Chapter 4

Don’t Sweat the Syntax

Programming languages, like natural languages, have a vocabulary (lexicon) and rules of syntax(grammar) that you have to learn in order to communicate. Just as unfamiliar grammatical conventions can make learning a new natural language difficult, unfamiliar programming-language syntax can make learning to program difficult. English speakers learning Japanese have to get used to the fact that Japanese verbs generally come at the end of the sentence. With computer languages, the problem is made worse by the fact that computers are much less adept at handling lexically and syntactically mangled programs than humans are at grasping the meaning of garbled speech.

If you want to talk with computers, however, you’re going to have to learn a programming language. Just as you learn new natural languages to communicate with other people and experience other cultures, you learn a programming language to communicate with computers and other programmers and to express computational ideas concisely and clearly. The good news is that learning one programming language makes it a lot easier to learn others.

When you start learning to program, you may find yourself consumed with sorting out the lexical and syntactic minutiae of the programming language. You’ll have to look up the names of functions and operators and memorize the particular syntax required to invoke them correctly. You may end up spending obscene amounts of time tracking down obscure bugs caused by misplaced commas or missing parentheses. This is really too bad, because fooling around with commas and parentheses is not what computer programming is all about; furthermore, these annoyances can usually be avoided by using a text editor that checks for syntactic errors — dealing with such details is one of the things that computers are good at.

What is computer programming all about? It’s about solving problems with computers. Unfortunately, that may not be immediately apparent in an introductory course. More often than not in beginning programming assignments, instructors tell you what you’re supposed to compute — they solve the problems — and your job is simply to translate what you’ve been told into whatever language you’re learning.

4.1  Specifications and implementations

A programming assignment might describe a computation in terms of a recipe — first do this, then do that, and so on. Such a recipe is called an algorithm. Programming assignments are also likely to include descriptions of various computational objects called data structuresthat organize the information needed for a computation and calling conventions called interfacesthat specify how to use the programs you’re writing. Algorithms, data structures and interfaces can be described in natural language, and the resulting description is called a specification. The result of translating a specification into a given computer language is called an implementation.

The strategy of giving beginning programmers a specification and asking them to provide an implementation has some merit. Once you’ve mastered the conventions of a given programming language you can start writing programs and interacting with the computer, and the more quickly you can start interacting with the computer, the more fun and positive feedback you’re likely to get. However, this strategy can discourage some people who might otherwise go on to become excellent programmers and encourage others who really aren’t well suited to programming. The problem is that a facility for mastering the syntax of programming languages is neither necessary nor sufficient to become a good programmer.

The hardest part of programming is transforming an initial, often vague description of what you want to do into a clear specification. If the specification is precise enough, then producing an implementation is relatively straightforward. Good programmers are, first and foremost, good problem solvers. If you like solving problems but are having some trouble getting over the initial hurdle of arcane syntax, don’t get discouraged, you can overcome the syntactic irritations with a little perseverance.

Here is an example of the problem-solving part of programming. You’ve probably heard dire warnings about letting interest charges on credit cards accumulate. The basic idea is that compounding interest can cause an initially small unpaid balance to balloon so that the next thing you know you’re up to your ears in debt. Suppose you want to understand this phenomenon more quantitatively. Specifically, you want to calculate what you would owe the credit card company after some number of months given an initial balance, a fixed interest rate, an estimated monthly payment, and an estimated monthly amount of new charges. One approach is to think about the computation as simulating the process whereby payments are made, interest accumulates and new charges appear on your monthly statement.

Here’s a natural language specification for this computation. Break the problem down into two cases. In the first case, there are no months left to simulate. This is the trivially easy special case in which you want to calculate what you owe after zero months. If the number of months is zero, then your computation should return the current balance. In the second case, there is at least one month left to simulate. To handle this case, you calculate a new balance, taking into account the interest, payments and charges for one month, and then consider the new problem of calculating what you would owe after one month less than originally specified, starting with the new balance.

This is called a recursive definition(recall our introduction in Chapter 1 to recursive rules in Prolog) because you repeatedly break a problem down into smaller parts and apply the same method to all the parts. Eventually the parts are so simple there is no need to break them down any further. In our example, each time you recursively consider the problem, the number of months decreases until eventually you reduce the problem to the trivially easy case.

Implementing this specification in the syntax of a given programming language may seem daunting at first, but it’s really just a matter of using some admittedly rigid conventions to make sure that a linguistically challenged, literal-minded computer does the right thing. You have to specify a name for the procedure that performs the calculations — call it debt. You also need names for the arguments referring to problem parameters such as the current balance, interest rate, estimated payment, estimated charges and number of months — call them, respectively, balance, rate, payment, charges, months. Finally you have to specify the logic and flow of control for the computation. Here a simple if-then-else construction will work fine. The recursive call requires some simple math functions to compute the balance after one month, but they’re relatively straightforward once you’re clear about the calculations.

Here’s what the full specification might look like in natural language:

Define the procedure debt as follows: The procedure is called with five arguments, balance, rate, payment, charges and months. If months is equal to zero, then exit the procedure, returning the value of balance. If months is not equal to zero, begin by introducing two new variables, new-balance and remaining-months. Let new-balance be the sum of charges plus balance plus balance times one-twelfth the interest rate minus payment. Let remaining-months be months minus one. Call the procedure debt recursively with the arguments new-balance, rate, payment, charges, and remaining-months. The value returned from this recursive call to debt is the value returned to the initial call to debt.

Once you’ve got the specification in this form, the next step really is easy, or rather will become so with some practice in the language you’ve chosen for implementation. Here’s an implementation written in the Scheme language we introduced in Chapter 1; it lacks some bells and whistles (for example, it might be a good idea to check that months is a non-negative integer), but you get the basic idea:

(define (debt balance rate payment charges months)
  (if (= months 0)
      balance
    (let ((new-balance (+ charges
                          balance 
                          (* balance (/ rate 12))
                          (- payment)))
          (remaining-months (- months 1)))
      (debt new-balance
            rate
            payment
            charges
            remaining-months))))

If I were writing this for my own use, I would dispense with the intermediate variables new-balance and remaining-months, inserting the expressions for their values (as specified in the let statement) directly in the recursive call as shown in the next definition. If the calculations are complicated enough, however, I generally do like to introduce intermediate variables to make the code more readable. Many programmers aspire to writing code that’s as readable as natural language.

(define (debt balance rate payment charges months)
  (if (= months 0)
      balance
    (debt (+ charges
             balance 
             (* balance (/ rate 12))
             (- payment))
          rate
          payment
          charges
          (- months 1))))

Just to test it out, if you start with an initial balance of zero and a fixed interest rate of 18% per year, and expect to pay $50 per month on $100 worth of purchases per month, then after four years or 48 months, you’ll owe:

> (debt 0 0.18 50 100 48)
3478.2609643766245

a little over $1000 of which is interest:

> (- (debt 0 0.18 50 100 48) (* 50 48))
1078.2609643766245

You’ll probably get this program wrong the first time, but even so, if the specification is correct, then you’re well on your way to solving the problem. My point is that the last step, converting the problem specification into an implementation in a particular programming language, is (or will soon become as you work with the language) the easiest and most automatic part of the whole process.

It’s also important to realize computer programming is as much about reading programs as it is about writing them. It’s useful to learn how to scan a program, even one in an unfamiliar language, in order to extract the gist. This ability to scan and extract summaries of technical specifications has its analog in every scientific and engineering discipline, whether the relevant specifications are text-based or graphical.

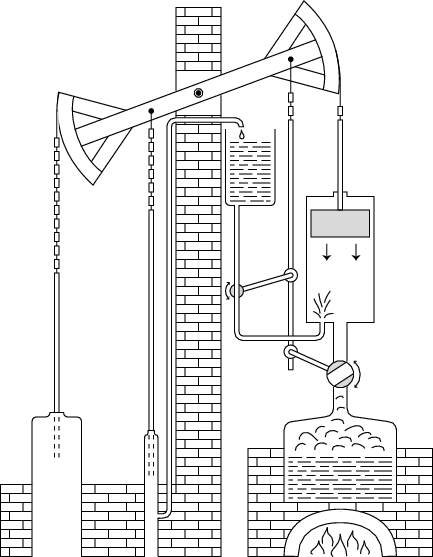
Think about how you’d make sense of the schematic in Figure 5 illustrating Thomas Newcomen’ssteam engine used in the 1700s to pump water from mines. You can probably figure out how the up-and-down action of the piston on the right translates into an up-and-down action of the shaft on the left pumping water from the mine. However, you might have to look at the diagram carefully and draw on your understanding of physics to understand the role of steam in supplying the motive force.¹

Some programmers think about programs linguistically. They analyze or parse programs in terms of sentences, words and parts of speech and think of constants as proper nouns, variables as pronouns or generic nouns that have different meanings depending on context, and procedures as imperative verbs. They develop an ability to squint at unfamiliar syntax, scan for the verbs and nouns and ignore the analogs of the “uhs” and “umms” punctuating everyday speech. Every parenthesis and semicolon in a computer program conveys some meaning, but some of the syntax doesn’t contain enough information to bother puzzling over.

With practice, you’ll get used to extracting the gist of unfamiliar syntax. Hardly a day passes that some piece of arcane syntax doesn’t whiz past as I’m invoking, installing, compiling and otherwise talking with machines. Happily, I rarely have to go back and figure out what the mysterious character sequences mean.

4.2  Syntactic variations across languages

I can’t say, however, that a facility for working with different programming languages and hence an ability to deal with syntax is unimportant. Professional programmers often have to deal with several languages in developing a given application. After a while, you learn to look past the syntax to the underlying meaning.

Let’s take a particularly simple program written in Scheme and consider its syntax in more detail. The factorial function, notated n! and spoken “n factorial,” takes a non-negative integer as its only argument and returns 1 for n = 0 or the product of 1, 2, 3, ..., up to n, for n > 0; thus, 4! = 1 * 2 * 3 * 4 = 24. Practically speaking, n! is the number of ways of ordering n items. Most large programs rely on libraries full of mathematical functions like factorial for everything from document formatting to financial planning.

Here’s how we might write factorial in Scheme:

(define (factorial n) 
   (if (= n 0) 
       1 
       (* n (factorial (- n 1)))))

As in the earlier example, I’ve defined factorial recursively. Mathematical expressions in Lisp and Scheme in particular are written in Polish notation, with the operator appearing first; thus instead of writing (3 + (3 * 3)), where the parentheses are optional, you would write (+ 3 (* 3 3)) and the parentheses are required by Scheme syntax.

Let’s make sure that our implementation works:

> (factorial 3) 
6 
> (factorial 4) 
24 
> (factorial 5) 
120
> (factorial 6) 
720 

Seems OK, but given my earlier warning you might be suspicious about negative numbers. The factorial of a negative integer is rarely useful and you’ll usually generate an error if you try to compute - 3 factorial in, say, a financial program. If you tried to compute (factorial -3) as defined, the computation would not terminate or would terminate with an error. A better implementation would test for a negative argument and terminate the computation with an informative error message, but we won’t worry about such niceties now. For present purposes, our simple definition is easy to understand and illustrates some points about Lisp syntax in particular and programming language syntax more generally.

In the definition of factorial, the definetells the computer that we’re about to define a function. The expression (factorial n) immediately following the define specifies the name of the function — factorial, the number of arguments — one in this case, and how the arguments are to be referred to in the function definition — the single argument is referred to as n. The expression (if (= n 1) 1 (* n (factorial (- n 1)))) is the function definition and specifies how the computation is to be carried out. In English, the specification reads as follows: if n is equal to 1 then return the value 1, otherwise return the value of n times the value returned by recursively calling factorial with the argument n minus 1.

Here’s a variation on factorial in which we’ve adopted a different syntax for calling functions, function( arguments ) instead of (function arguments), infix notation (n == 1) instead of prefix notation (= n 1), and different primitive functions and predicates, == instead of = for numerical equivalence. We’ve eliminated the define so we’ll have to make sure that the computer doesn’t confuse this definition with some other sort of specification.

factorial( n ) 
   if ( n == 0 ) 
      1
      n * factorial( n - 1 )

Without indentation, this definition could be interpreted in a number of ways. In particular, without indentation, it’s not clear which expressions correspond to the various parts of the if-then-else statement. In the next variation, we use curly brackets and semicolons instead of parentheses to set off statements and larger blocks of code, and we use the keyword else to identify the else part of the if-then-else statement:

factorial( n ) {
   if ( n == 0 )
      1;
      else n * factorial( n - 1 );
}

Many languages require the programmer to specify the typeof each variable and the type of the values returned by each function. For example, integer, string and character are primitive types available in most programming languages. Scheme doesn’t require such a specification. Also, some languages require that a function definition explicitly indicate what the function returns. In the next variation, we make use of the return keyword and introduce a variable result to keep track of the returned value of the factorial function. We use the int type specifier to indicate the type of n and result as well as the type of the result returned by factorial. Note that == is a predicate used to test for equivalence, while = is the assignment operator (not to be confused with the Scheme predicate) that assigns the variable appearing on the left-hand side of the operator to the value of the expression on the right-hand side. Finally, the indentation and formatting of the function definition have been adjusted slightly to suit the prevailing conventions for this sort of syntax.

int factorial( int n ) {
       int result;
       if ( n == 0 )
          result = 1;
       else result = n * factorial( n - 1 );
       return result;
}

We’ve transformed our Scheme definition of factorial into code written in a different language. This program fragment would work as part of a program in Java or C.We’d need to wrap it in some additional syntax to run it, but the actual definition is complete.

Here’s how the code fragment might appear in a complete Java program that simply prints out the value of 3!:

class Factorial {
   public static void main( String[] args ) {
       System.out.println( factorial( 3 ) );
   }
   public static int factorial( int n ) {
       int result;
       if ( n == 0 )
           result = 1;
       else result = n * factorial( n - 1 );
       return result;
   }
}

Running this program takes a few additional steps. Assuming that the code resides in a file called Factorial.java, now I display the code using the Unix cat command, compile it using the Java compiler javac, and then run it using the Java interpreter java (I typed everything to the right of the % prompt and the various programs are responsible for the rest):

% cat Factorial.java
class Factorial {
   public static void main( String[] args ) {
       System.out.println( factorial( 3 ) );
   }
   public static int factorial( int n ) {
       int result;
       if ( n == 0 )
           result = 1;
       else result = n * factorial( n - 1 );
       return result;
   }
}
% javac Factorial.java
% java Factorial
6

If I were working in C, the wrapper code would be somewhat different and the steps of compiling and invoking the program would be different, but not that much:

% cat factorial.c
main () {
   printf("%d\n", factorial( 3 ) );
}

int factorial( int n ) {
       int result;
       if ( n == 0 )
          result = 1;
       else result = n * factorial( n - 1 );
       return result;
}
% cc -o factorial.o factorial.c
% factorial.o
6

The point is that after a while the syntax won’t matter that much to you. You’ll use an editor to write programs, you’ll submit your programs to other programs, compilers and interpreters that will convert them into a form that can be directly run a computer and then you’ll execute those programs. The steps may vary but the basic idea remains the same. The hard part, indeed the creative part, is coming up with the specifications that solve problems. After some years of practice, if you stumble on a program written in a language you’re not expert in, say Mathematica,

In[1]:= factorial[n_Integer] := If[n == 0, 1, n * factorial[n - 1]]

In[2]:= factorial[3]

Out[2]= 6

you’ll just squint at the unfamiliar notation and after a couple of lines say, “I get it! It’s just the factorial function in yet another syntactic variation — no sweat.”

4.3  Stylistic variations across implementations

Variations across languages are just one source of variability in implementing specifications. Even within a particular language there are typically many different ways of writing even the simplest of functions. Here’s an implementation of the factorial function using the Java/C syntax and employing an iterative rather than recursive strategy:

int factorial( int n ) {
       int result = 1;
       for ( int i = 2; i <= n; i++ ) {
           result = result * i;
       }
       return result;
}

An integer counter is introduced in the “for loop” to count down from n to 2.

Here’s another implementation using a different iterative construct (a “while loop”) and making the argument variable do double duty as the counter:

int factorial( int n ) {  
       int result = 1;
       while ( n > 1 ) {     
           result = result * n;
           n = n - 1;          
       }                     
       return result;          
}     

And here’s an alternative implementation in Scheme using an additional function to introduce counter and result variables. While the auxiliary function includes a recursive call, this implementation is really more in the spirit of the first of the two iterative implementations:

(define (factorial n)
   (aux-factorial 1 1 n))

(define (aux-factorial result i n)
   (if (> i n)
       result
       (aux-factorial (* result i)
                      (+ i 1)
                      n)))

In time you’ll find a programming style that suits you, probably using different strategies as the situation warrants and your aesthetic sense dictates. Even as writers search for the right word, the phrase that most perfectly conveys their thoughts, so programmers look for the implementation that most elegantly solves the problem. Might not sound like a high art form to you, but programming is definitely a craft with its own aesthetic.

4.4  Developing a facility for language

You might think that to learn a new programming language you buy a book describing its syntax and then slog through the chapters until you understand all the details. Perhaps some programmers learn this way, but most people learn new programming languages the same way they learn new natural languages: by learning to say the things they want or need to say and attending to the differences between languages.

If you’re learning C and you know Scheme, you’ll probably want to figure out how to translate (define (function arguments) definition) into function( arguments ) { definition }. If you’re learning Mathematica and you know C, you’ll be interested in turning for ( start; test; increment ) { body } into For[ start, test, increment, body ]. Most of us aren’t interested in communicating syntax, we’re interested in communicating meaning.

Learning your first programming language is a bit like learning your first natural language; it takes time, patience and a willingness to experiment. And, while the range of meaning you can convey in a programming language is virtually unlimited, expressing a particular idea so that a computer can understand it can be pretty painful. If you want to tell a robot to walk down the hall and turn left at the corridor with the ugly beige carpet, you’re going to have to write a lot of statements of the form for ( int i = 1; i < n; i++ ) { ... }.

To program a computer you have translate your way of thinking about the world into primitive operations like adding and multiplying numbers, testing if a number is zero and using if-then conditional statements to control execution. Once you understand how to combine these primitive operations to do more complicated calculations, you’re on the road to becoming a computer programmer — the syntax really has very little to do with it. Instead of thinking of the computer as a parent teaching you how to communicate with it, you’ll be teaching the computer by building a vocabulary that will let you rise above the primitive operations and enable you to communicate fluidly.