Getting Oriented
On the morning I began this chapter, I was driving into work and passed a sign near a grade school advertising a “Bug Safari”. When I got to work, I found out from the Web that “Butterfly Walks”, “Spider Safaris”, “Pond Dips” and similar excursions are regular fare at summer camps and neighborhood activity centers. This intrigued me: who would lead these tours? I initially thought that the most likely candidates would be trained entomologists or specialists such as lepidopterists. An entomologist studies bugs, beetles, butterflies, spiders and the like (not to be confused — as I usually do — with the similar-sounding etymologist, someone who studies the derivation of words), while lepidopterists specialize in lepidoptera, butterflies and moths.
But then I realized that it’s a rare specialist who can resist being distracted by his or her own specialty. I thought about what this tendency might portend for my attempt to speak to a general audience about concepts in computer science. By most accounts, I’m an expert in computer science and a specialist in artificial intelligence. But just as a trained and practicing physicist is not an expert in all matters spanning the length and breadth of physics, from quantum electrodynamics to cosmology, so I’m not an expert in all areas of computer science.
In this chapter, I’ll be talking about programming languages, an area of computer science about which I know a fair bit but certainly am not an expert. As your guide for today’s “Computational Safari”, I’ll introduce you to some interesting programming-language flora and fauna, but don’t be surprised if my interest in artificial intelligence biases my choice of topics. Programming languages often spring from the needs of particular areas of computer science, and artificial intelligencehas been a driving force in the creation of many languages including Lisp, Scheme and, as we’ll see, various object-oriented languages.
6.1 Structuring large programs
In Chapter 5 we encountered the substitution model. In a purely theoretical sense, this model provides all the power or “expressiveness”you’ll ever need. Computational models are often characterized in terms of their expressiveness, the extent to which they allow you to express or specify computations. One model, call it the plain vanilla model, is less expressive than a second model, call it vanilla with savory chocolate bits, if, say, you can specify how to add numbers of any size in the vanilla-with-chocolate-bits model but only how to add numbers less than 1,000 in the plain vanilla model.
Although the substitution modelis as powerful as any computational model can be, models have characteristics apart from power that differentiate them. Paramount among these characteristics are simplicity, comprehensibility, and the ability to organize or structure large programs. The substitution model is certainly simple to learn and easy to comprehend, but it doesn’t help particularly in structuring large programs.
The first thing you should realize when considering a large program is that any program of, say, several tens of thousands of lines of code is likely to have been written by more than one programmer. Even if it was written by one person, most merely mortal programmers can’t keep all the details in a large software project in their heads at the same time, so it’s almost as though there are several programmers. The way most professional programmers deal with large amounts of code is to break it down into smaller chunks, called variously libraries, packages, classes, and modules.
Each chunk is designed to provide a particular service or solve a particular part of the overall problem. The application programming interface(API) of a given chunk specifies how programs can use the functionality provided by that chunk. The API for a library that supports drawing geometric diagrams might include instructions on how to draw rectangles or circles on your screen; these parts of the geometry library are made “public” so that other programmers can use them.
In order to implement a geometry library you might also need a lot of support functions, say functions that use trigonometry to rotate and redraw rectangles, that aren’t part of the library’s interface. These trig functions are considered “private.” The programmer using a library knows only the public procedures specified in its API. The author of a library is free to rewrite the internals of the library and, in particular, to rewrite or rename its private functions.
In addition to hiding unnecessary detail from the programmer, this method of breaking large problems into bite-sized chunks allows groups of programmers to work together, share code (APIs at least) and improve existing libraries without interrupting one another. In theory, a team of programmers can partition a large project into a bunch of interacting modules, specify the interfaces for the modules and then go off and work independently to write the internals of their respective modules. In practice, large software projects require almost constant communication among the developers.
Libraries and modules also establish a discipline for naming things. Within a library you can use any names you like for private functions as long as you’re consistent within that library. Someone else writing the internals of another library can use the same names with no fear of confusion. Two libraries can use the same public name. For example, both the geometry library and the euclid library may have functions called circle that perform different operations. If you want to use both libraries in the same program, you have to disambiguate your use by indicating the context somehow, say by appending the library name, so that geometry::circle is unambiguously different from euclid::circle. All this may seem a little picayune when you’re just starting out, but such common-sense conventions are essential in building large programs.
This is an example of what happens when you hire a myrmecologist (someone who studies ants) to lead a bug safari and then run into a bunch of interesting moths — you’ll probably get some useful information about moths but not the same sort of information you’d have gotten had you hired a lepidopterist. I no longer write large programs, though I commonly write programs that use several libraries. Occasionally I write a library myself; you get a sense after a while of when it makes sense to take a chunk of code and turn it into a separate library. I’ve never worked as part of a team of programmers to develop a large project as a set of loosely coupled modules whose interaction is completely specified by their respective APIs, but it seems a perfectly reasonable way of proceeding and my students and professional programmer friends tell me it works (much of the time). We’ll get back to libraries in Chapter 7, but in the meantime there’s a fascinating little ant colony I’d like to explore.
6.2 Procedures that remember
This cursory overview of what’s involved in structuring large programs emphasized techniques for avoiding cognitive overload in programmers, avoiding conflicts in naming and separating the public and private parts of larger software components. The substitution model (or at least the simple version in Chapter 5) does little to support our thinking about such issues in part because it assumes such a simple model of memory.
Where does memory come up in thinking about programming? When you type a set of define statements to a Scheme interpreter, you essentially create a set of associations in memory. In the next exchange, I define a function for converting inches to centimeters, specify a conversion rate and invoke the function on my approximate height in inches to obtain my height in centimeters:
> (define (inches_to_centimeters x) (* x conversion_rate)) > (define conversion_rate 2.54) > (inches_to_centimeters 73) 185.42000000000002
The function name inches_to_centimeters and the constant conversion_rate are said to be “global” in the sense that they can be seen (referred to) by any other function I might define. What if I wanted conversion_rate to be “local” to inches_to_centimeters in the sense that it was seen only by the inches_to_centimeters function?I could do this by defining inches_to_centimeters as:
> (define inches_to_centimeters
(let ((conversion_rate 2.54))
(lambda (x) (* x conversion_rate))))
There’s a lot going on in this little function, so we’ll take our time exploring it. As usual, the syntax is a pain but we’ll work our way through it. If you paid really close attention in Chapter 5, you might recall some odd facts about define, namely that (define name body) evaluates body and assigns the result to name, while (define (name args) body) stores body along with the calling pattern (name args) in the definition of name and trots out body as a recipe for the computation assigned to name whenever Scheme is asked to evaluate something of the form (name args). You might want to read that again.
The lambda(referring to the Greek letter and hinting at the mathematical origins of Lisp in theoretical computer science) is like the single- and double-quote mechanisms for controlling evaluation that we met in discussing shell scripts in Chapter 2. lambda says to the Scheme interpreter, “Stop evaluating! I’m a recipe for a procedure; set me aside until you want to apply this recipe to an appropriate set of arguments.”
This distinction between “evaluate now” and “store in order to evaluate later” is important, and I admit that it would be nice if Scheme made it more syntactically obvious. The definition (define (name args) body) is semantically the same as (define name (lambda (args) body); for example, (define square (lambda (x) (* x x))) and (define (square x) (* x x)) are interpreted in exactly the same way.
So, from what I just said, Scheme will evaluate (let ((conversion_rate 2.54)) (lambda (x) (* x conversion_rate))), but when it gets to the (lambda (x) ...) it’ll stop evaluating. What happens when Scheme evaluates the (let (...) ...) part? When Scheme evaluates an expression of the form (let (variable-value-pairs) body) it sets aside a portion of memory in which to keep track of the variables and their specified values, but these variables are visible only to the expressions in the body of the let statement.
With that lengthy prologue, our definition (define inches_to_centimeters ...) can be paraphrased as follows: I’m defining a function called inches_to_centimeters, and in doing so I’m going to introduce some special terminology so that, only in the context of this definition, the variable conversion_rate refers to the number 2.54. Other functions won’t be able to see inches_to_centimeters’s local conversion_rate, and indeed they can feel free to define their own local variables with the same name if they so choose. Another way of thinking about this is that I’m allocating some space in my memory for the definition of inches_to_centimeters and, along with the space for the definition, I’m setting aside space for a constant to be seen only by inches_to_centimeters.
Well, the basic idea seems pretty useful but applying it in this particular case doesn’t make a whole lot of sense. The way I’m using conversion_rate in inches_to_centimeters, I could have just as easily defined it as:
> (define (inches_to_centimeters x) (* x 2.54))
But there are other cases in which setting aside a private memory area to keep track of things makes lots of sense. To illustrate, we’ll need some way to change the contents of memory. If you think of let as the way of setting aside or allocating portions of memory, then set! is the way to change the contents of portions of memory within the let statement that allocated them. When it comes to memory, we want to be able to forget as well as remember, change our minds as well as make up our minds. Once you can alter memory, things get more interesting.
Just for fun, we’re going to make up a tricky little program that multiplies pairs of numbers. The reason it’s a bit mischievous is that it returns not the product of the two numbers it’s given as arguments but the product of the two numbers that were given the previous time the function was called.
> (define behind_the_times
(let ((x 0) (y 0) (z 0))
(lambda (a b)
(set! z (* x y))
(set! x a)
(set! y b)
z)))
The (set! term expression) allows us to change the contents of memory (the specific location in memory in this case is referenced by term) to refer to the result of evaluating expression. And so we get this behavior:
> (behind_the_times 1 3) 0 > (behind_the_times 2 3) 3 > (behind_the_times 3 4) 6
Now a multiplication function that returns the result of multiplying the previous pair of numbers it was given is not terribly useful, but behind_the_times is definitely a function with a memory. I’m sure you can imagine a better application — say, a function that keeps track of your bank balance or remembers the answers to particularly difficult problems and returns them instantly when asked again (such functions are said to be memoized).
So let allows us to allocate or lay aside portions memory and associate these portions of memory with function definitions, and set! allows us to modify the contents of memory. The lambda syntax is just another way of providing the definition of a procedure (lambda (args) body), where body is the full description of the function. But it also gives us a powerful way of extending functions. What do you think the next definition does?
> (define (head contents)
(let ((memory contents))
(lambda (what)
(if (equal? what "more")
(set! memory (+ memory 1))
(if (equal? what "less")
(set! memory (- memory 1))
(if (equal? what "show")
memory))))))
I hope the equal? didn’t distract you: it’s like = except that it checks whether two items are the same when the items are something other than numbers. The notion of equality is complicated even for numbers — is the integer 0 equal to the “real” number 0.0? — but we won’t sweat the details here. Using equal? we can compare strings, which in Scheme are set off by double quotes.
In any case, equal? wasn’t the tricky part. The tricky part is that every time the function head is called it returns a brand-new function with its own specially set-aside portion of memory for storing a local value of contents. In order to understand what is really going on in the last definition, it might help to use the alternative syntax for defining functions, (define name (lambda (args) body), and think about what gets evaluated when:
> (define head
(lambda (contents)
(let ((memory contents))
(lambda (what)
... ))))
The head function creates other functions:
> (define freds_head (head 17)) > (define annes_head (head 31)) > (freds_head "less") > (annes_head "more") > (freds_head "show") 16 > (annes_head "show") 32
We used head to create freds_head and annes_head as distinct functions with their own separate associated memory. The variable contents in the context of freds_head is completely different from the variable contents in the context of annes_head. The two functions freds_head and annes_head are completely separate and retain a memory of their past in the form of their local version of contents.
We can use head to create as many of these functions as we like. You can even define functions with their own local functions:
> (define cerberus
(let ((dopeys_head (head -7))
(sleepys_head (head 0))
(grumpys_head (head 7)))
(lambda (which what)
(if (equal? which "dopey")
(dopeys_head what)
(if (equal? which "sleepy")
(sleepys_head what)
(if (equal? which "grumpy")
(grumpys_head what)))))))
> (cerberus "dopey" "less")
> (cerberus "grumpy" "more")
> (cerberus "dopey" "show")
-8
> (cerberus "grumpy" "show")
8
Well, you get the idea. We just defined a function cerberus that has as part of its local memory three newly minted head-generated functions, dopeys_head, sleepys_head and grumpys_head, each of which has its own private contents.
Using lambda and let, you can create functions that are said to be “first-class objects” — objects with their own mutable memories (they’re said to have “internal state”) and their own varied set of capabilities (called “methods”) embodied in their associated functions. Such objects are the basis of a powerful programming model called object-oriented programmingthat supports software engineering in the large, the art and science of building large programs. Objects with internal state and associated methods can create more versatile spirits. Now our procedures can give rise to spirits that persist over time, have memory and can even cast their own spells by creating and invoking new procedures.
6.3 Object-oriented programming
In the previous section, we beefed up procedures to have persistent memory (internal state) and their own specially assigned internal procedures. Using lambda and let, we can mix and match procedures and internal state. We can define a group of procedures that share state so that any of the procedures can refer to (read) or modify (write) their shared locations in memory but no procedures outside the group can read or write to these locations.
An object in object-oriented programming sometimes behaves like memory and sometimes behaves like a procedure or, rather, a whole passel of procedures. Imagine a procedure called make_room that takes two arguments, integers corresponding to the width and length of a room in inches, and returns a “room object”:
> (define annes_living_room (make_room 7 8))
We could ask annes_living_room to tell us its width or compute its area:
> (annes_living_room "width") 7 > (annes_living_room "area") 56
It might even be smart enough to convert its default metric units, say square meters for area, to imperial units, square yards in this case:
> (annes_living_room "area" "imperial") 66.98
We could change the dimensions of the room, read or write the width and length in any units, ask annes_living_room to, say, display itself as a rectangle in a graphical interface or alter how it’s displayed, say, by rotating the rectangle a specified angle in a specified direction about its centroid. We could combine the annes_living_room object with, say, annes_kitchen object to create a composite object with associated composite information and compositing procedures. In general, annes_living_room would be a single source for information about Anne’s living room and procedures for doing things with and to this information.
This syntax is pretty clunky, but it’s just syntax, and the syntax for object-oriented languages like C++ and Java looks pretty clunky the first time you see it. For instance, in Java, we might create a new room and assign it to the variable annes_living_room with the incantation:
annes_living_room Room = new Room (width.7,length.8) ;
refer to the width of this room in a program as:
annes_living_room.width
refer to (compute in this case) the area of annes_living_room as:
annes_living_room.area
refer to the area in alternative units of measure as:
annes_living_room.area("imperial")
and perhaps request that annes_living_room “rotate itself” 180 degrees counterclockwise (-Pi radians) and then “draw itself” at coordinates 500 by 500 in some (unspecified) graphics window as:
annesLivingRoom.rotate(- Pi) ; annesLivingRoom.draw(500, 500) ;
The syntax doesn’t really matter that much. What matters is that objects have state and can perform all sorts of useful computations; you tend to stop thinking of them as data or procedures and start thinking of them as repositories of a particular sort of knowledge or expertise. Some programmers like to think of objects as entities to which you can send requests to provide services. Objects often refer to other objects and may even have a set of objects exclusively cached away in their internals; for example, a chess-board object might have a collection of objects corresponding to chess pieces. It’s a very powerful way of thinking about programs and, as I mentioned in the previous section, it’s the basis of an engineering discipline for the design and development of very large programs consisting of millions of lines of code.
There’s another aspect of object-oriented programming that I’ll mention in passing, as it is often touted as one of the principal useful characteristics of this model of computation. In Java and C++, programs are organized in terms of classes. A class is like a library in that it provides a particular set of capabilities. But not only can you generate instances of a class and thereby directly take advantage of its capabilities, you can also extend the class by adding new capabilities or altering existing ones.
Imagine that we have a class called Rectangle that has a width and length and can be drawn in a graphics window, rotated, resized and, perhaps, labeled, shaded and painted different colors. Now I want to create a Room class that computes its area, handles conversions, performs functions peculiar to my program, but otherwise behaves like an instance of the Rectangle class. Someone probably worked hard to create the Rectangle class and it doesn’t make sense for me to repeat this work and perhaps not even do as good a job.
In Java, C++, C#, Smalltalkor any number of other object-oriented programming language, I would define the Room class as a subclass of the Rectangle class that inherits most if not all of the capabilities of the Rectangle class. An instance of the Room class such as annes_living_room would behave like a Rectangle except in cases where I explicitly override a Rectangle capability. So I’ll be able to draw and rotate a Room without ever writing any code for these operations.
This is great if you’re smart or lazy or both. Before you write a program to do something, you look for a class that does most of what you want to do and then simply adapt it to your particular purposes by defining a new class that inherits what you want from the original class. Really well-written classes become widely used and programmers end up being much more efficient by reusing other programmers’ code.
6.4 Programming with constraints
You don’t need to use an object-oriented programming language to program in an object-oriented style or exploit the ability of object-oriented programming languages to structure large programs. My initial exposure to object-oriented programming came soon after I started using Lisp, first in a dialect called T and then later in a dialect called Zeta Lisp, both of which had object-oriented extensions. At that point, I found the object-oriented viewpoint more useful in understanding existing programs than in structuring my own.
When I discovered how to implement objects in Lisp, the big eye-opener for me was that I could invent my own languages and create my own syntax to suit the problem at hand or my own idiosyncratic perspectives on computing. I loved to create my own Lisp-implemented variants of object-oriented programming languages. Conversely, programming in Smalltalk, an early object-oriented language, changed how I thought about writing programs in Lisp. One of AlanPerlis82’s “Epigrams on Programming” reads, “A language that doesn’t affect the way you think about programming is not worth knowing” and, whether by accident or design, I’ve persisted in using and learning only languages that provided that added benefit.
Often, in the process of solving a particular problem you end up inventing a highly specialized language. In some cases, that specialized language is subsequently generalized to solve a wider range of problems. In the remainder of this chapter, we’ll explore an idea that inspired a new model of computation called constraint programmingand was an important influence on object-oriented programming languages.
Consider this simple algebra problem, a variant of the one that started us off thinking about the substitution model in Chapter 5:
The living room in Anne’s house is 56 square meters. She wants to buy a rug that fits exactly in the room. Along one side of the room is a 3-meter-wide fireplace flanked by two identical bookcases that together take up the entire width of the room. The bookcases are 2 meters wide each. The fireplace and two bookcases are built into the wall and don’t cover any floor space. What are the dimensions of the rug that Anne should buy?
We begin by noting the known and unknown quantities:
living_room_area = 56 bookcase_width = 2 fireplace_width = 3 living_room_width = fireplace_width + (2 * bookcase_width)
We have the same general relationship as before,
living_room_area = living_room_length * living_room_width
but it isn’t quite what we need, and so we do a little algebra to isolate the unknown variables on one side of the equation:
living_room_length = living_room_area / living_room_width
substitute the appropriate formula for items that have to be computed:
living_room_length = living_room_area / (fireplace_width + (2 * bookcase_width))
and then do the necessary calculations by plugging in the numbers and substituting the results back into the formula:
living_room_length = living_room_area / (fireplace_width + (2 * 2)) living_room_length = living_room_area / (fireplace_width + 4) living_room_length = living_room_area / (3 + 4) living_room_length = living_room_area / 7 living_room_length = 56 / 7 living_room_length = 8
This is all well and good, but we can’t use the same Scheme functions we defined in Chapter 5. Why? Because they handle only one particular case. Given the equation
living_room_area = living_room_length * living_room_width
and given values for any two of the terms, we can compute the third. Why can’t we simply provide this equation and have the computer figure out how to compute the missing value when two other values are supplied? A similar question occurred to Ivan Sutherlandback in the early ’60s when he was implementing Sketchpad, a system that anticipated a bunch of technologies we take for granted today, including graphical interfaces and an object-oriented programming style.
Sutherland was interested in displaying graphical objects and he wanted to specify general constraints (equations) governing their position and orientation and have the computer figure out the consequences of those constraints in drawing the objects on the computer screen. For example, at one point you might say that two rectangles should be drawn so that one is above the other, and later you might add that the bottom of one should be aligned with the top of the other and both enclosed in a third rectangle. The computer is expected to display these three rectangles so that all of these constraints are satisfied.
Later (1977) Alan Borningused the object-oriented language Smalltalk to develop an elegant design environment for computer simulations based in part on Sutherland’s ideas. And still later AbelsonandSussman85created a “constraint-oriented” language in Scheme and used it in their book Structure and Interpretation of Computer Programs. The code for Abelson and Sussman’s constraint-oriented language is available on the MIT Press web site, so I copied the relevant parts into a file called constraints.scm and then loaded the file into Scheme:
> (load "constraints.scm")
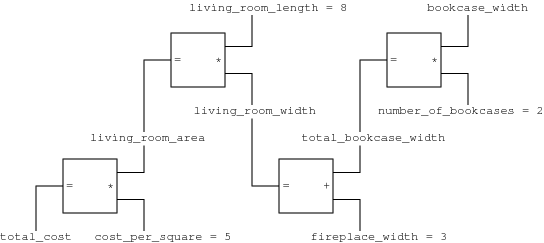
I created objects for each of the terms in the next equation, specified that they are related to one another through multiplication, and indicated that the cost per square meter is a particular constant value. The terms in the equation become connector objects that connect different constraints. The constraints for this application, called multipliers and adders for obvious reasons, are attached to the appropriate connectors. Here’s the equation:
total_cost = cost_per_square_meter * living_room_area
and here are the incantations that create the necessary connectors and constraints:
> (define total_cost (make-connector))
> (define cost_per_square_meter (make-connector))
> (define living_room_area (make-connector))
> (multiplier cost_per_square_meter
living_room_area
total_cost)
> (constant 5 cost_per_square_meter)
What would you guess that a multiplier constraint does? Think about a multiplier (or adder for that matter) as follows. Suppose that the living_room_area connector suddenly wakes up and realizes it knows its “value”. Well, that might be important information to send along to the multiplier created in the last exchange, so living_room_area wakes up the multiplier and says, “Hey! Here’s some new information, see if you can do something with it.” Perhaps the multiplier checks and finds out that neither cost_per_square_meter nor total_cost connectors have values; therefore it can’t do anything with the information, so it goes back to sleep. Alternatively, perhaps the multiplier finds that cost_per_square_meter has a value but total_cost currently doesn’t; so the multiplier figures out what the value of total_cost should be and tells the total_cost object to wake up and see if anyone else cares about this new value.
The multiplier doesn’t have to be too smart, just smart enough to handle these three special cases: If cost_per_square_meter and living_room_area have values, then set
total_cost = cost_per_square_meter * living_room_area.
If cost_per_square_meter and total_cost have values, then set
living_room_area = total_cost / cost_per_square_meter.
Finally, if living_room_area and total_cost have values, then set
cost_per_square_meter = total_cost / living_room_area
Now we’ll do something very similar with the next equation:
living_room_area = living_room_width * living_room_length
which results in the incantations
> (define living_room_width (make-connector))
> (define living_room_length (make-connector))
> (multiplier living_room_width
living_room_length
living_room_area)
> (constant 8 living_room_length)
And again, from the equation
living_room_width = fireplace_width + total_bookcase_width
we invoke
> (define fireplace_width (make-connector))
> (define total_bookcase_width (make-connector))
> (adder fireplace_width
total_bookcase_width
living_room_width)
> (constant 3 fireplace_width)
And finally, for the last equation
total_bookcase_width = number_of_bookcases * bookcase_width
we produce
> (define number_of_bookcases (make-connector))
> (define bookcase_width (make-connector))
> (multiplier number_of_bookcases
bookcase_width
total_bookcase_width)
> (constant 2 number_of_bookcases)
All the constraints are related to the other constraints they depend on through the connectors. Abelson and Sussman provide the abstraction of a probe that you can attach to a connector as though attaching an oscilloscope or voltmeter probe to a wire in an electrical circuit. The probe then reads off the value of the connector whenever it changes. We’ll put a probe on two of the connectors:
> (probe "bookcase width" bookcase_width) Probe: bookcase width = ? > (probe "total cost" total_cost) Probe: total cost = ?
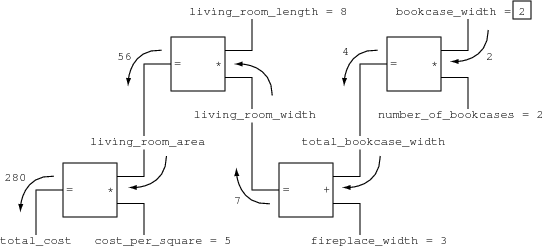
The reply from the interpreter indicates that the constraint system currently has no values for these terms. So let’s set one of them. We’ll try the easy case first (corresponding to the case handled by the simple functional solution we implemented in Chapter 5):
> (set-value! bookcase_width 2 'user) Probe: bookcase width = 2 Probe: total cost = 280 done
Works as expected. Let’s undo that last operation and then set the total cost to see if the constraint system can work backwards:
> (forget-value! bookcase_width 'user) Probe: bookcase width = ? Probe: total cost = ? done
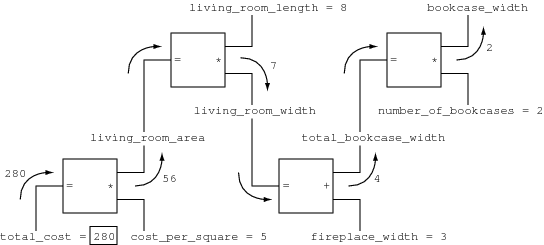
It looks like the values have returned to being unknown. So, let’s set total_cost to be 280 and see if the values propagate backward through the constraints to determine bookcase_width:
> (set-value! total_cost 280 'user) Probe: total cost = 280 Probe: bookcase width = 2 done >
|
That’s the answer we were looking for: propagating the constraints calculates the right values as long as there is enough information to do so. By the way, why do you think that the probes responded in a different order this time? Recall that a probe reads off the value of its connector only when that value changes. The order of computation is determined in all cases by the topology of the connections and constraints.
Figure 7 clarifies the order of computation and the way in which the constrained values are propagated through a constraint network. Figure 7a shows the constraint system with only the constants assigned values. No constraint propagation is possible in this case. Figure 7b shows the propagation that results from setting total_cost to 280, assuming that bookcase_width is not assigned a value. In this case the multipliers are solving for x in x + y = z given y and z, and analogously for the single adder. Figure 7c shows the propagation that results from setting bookcase_width to 2, assuming that total_cost is not assigned a value. In this case the multipliers are solving for z in x + y = z given x and y, and analogously for the single adder.
The code fragments used to create and then alter the constraint systems illustrate another model of computation, based on the propagation of constraints and inspired or at least facilitated by thinking in terms of object-oriented programming. In our example, the terms in the equations for our simple algebra problem are animated as objects that can receive instructions, for example, set-value! 280, consult their internal state, send instructions to other objects, and set in motion complicated computations that ripple through a set of objects.
As I mentioned earlier, when you hire a myrmecologist as a field guide you’re likely to learn more about ants than spiders or bees. I’m more expert in artificial intelligence than in programming languages, but programming languages influence how you think about whatever it is you write programs for. If the programs you write always seem to have the same structure or involve the same blocks of code with only small variations, pretty soon you start thinking about writing a special-purpose language to make writing them easier and more natural.
The fields of artificial intelligence, robotics and computer graphics all involve different ways of thinking about computation. Programming languages based on the propagation of constraints have arisen out of several different fields. Occasionally, some core idea found in a language or a set of related languages cries out to be generalized and codified in a set of syntactic conventions that make it easy to adopt a particular way of thinking about computation. Object-oriented programming is one such core idea; in fact, it comprises a set of core ideas that have wide appeal and turn out to be very useful for software engineering in the large.