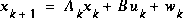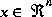,
of a first-order, discrete-time controlled process that is governed by the linear difference equation
,
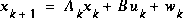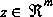that is
.
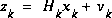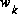and 
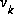represent the process and measurement noise (respectively). They are assumed to be independent (of each other), white, and with normal probability distributions
,
.
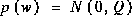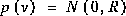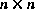matrix A in the difference equation (1.1) relates the state at time step k to the state at step k+1, in the absence of either a driving function or process noise. The 
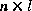matrix B relates the control input 
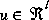to the state x. The 
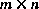matrix H in the measurement equation (1.2) relates the state to the measurement zk.
The Computational Origins of the Filter
We define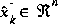 
(note the "super minus") to be our a priori state estimate at step k given knowledge of the process prior to step k, and 
to be our a posteriori state estimate at step k given measurement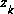 
. We can then define a priori and a posteriori estimate errors as
The a priori estimate error covariance is then
(1.5)
and the a posteriori estimate error covariance is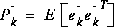
, (1.6)
In deriving the equations for the Kalman filter, we begin with the goal of finding an equation that computes an a posteriori state estimate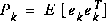 
.
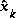as a linear combination of an a priori estimate 
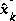and a weighted difference between an actual measurement 
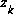and a measurement prediction 
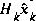as shown below in (1.7). Some justification for (1.7) is given in "The Probabilistic Origins of the Filter" found below.
(1.7)
The difference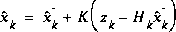 
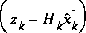in (1.7) is called the measurement innovation, or the residual. The residual reflects the discrepancy between the predicted measurement 
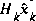and the actual measurement 
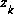. A residual of zero means that the two are incomplete agreement.
The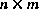 
matrix K in (1.7) is chosen to be the gain or blending factor that minimizes the a posteriori error covariance (1.6). This minimization can be accomplished by first substituting (1.7) into the above definition for 
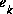, substituting that into (1.6), performing the indicated expectations, taking the derivative of the trace of the result with respect to K, setting that result equal to zero, and then solving for K. For more details see [Maybeck79], [Brown92], or [Jacobs93]. One form of the resulting K that minimizes (1.6) is given by
(1.8)
Looking at (1.8) we see that as the measurement error covariance 
.
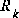approaches zero, the gain K weights the residual more heavily. Specifically,
On the other hand, as the a priori estimate error covariance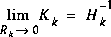 
.
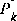approaches zero, the gain K weights the residual less heavily. Specifically,
Another way of thinking about the weighting by K is that as the measurement error covariance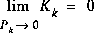 
.
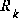approaches zero, the actual measurement 
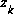is "trusted" more and more, while the predicted measurement 
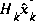is trusted less and less. On the other hand, as the a priori estimate error covariance 
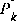approaches zero the actual measurement 
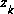is trusted less and less, while the predicted measurement 
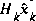is trusted more and more. The Probabilistic Origins of the Filter
The justification for (1.7) is rooted in the probability of the a priori estimate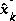 
conditioned on all prior measurements 
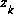(Baye's rule). For now let it suffice to point out that the Kalman filter maintains the first two moments of the state distribution,
The a posteriori state estimate (1.7) reflects the mean (the first moment) of the state distribution¯ it is normally distributed if the conditions of (1.3) and (1.4) are met. The a posteriori estimate error covariance (1.6) reflects the variance of the state distribution (the second non-central moment). In other words,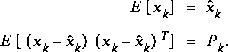
For more details on the probabilistic origins of the Kalman filter, see [Maybeck79], [Brown92], or [Jacobs93].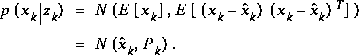
. The Discrete Kalman Filter Algorithm
I will begin this section with a broad overview, covering the "high-level" operation of one form of the discrete Kalman filter (see the previous footnote). After presenting this high-level view, I will narrow the focus to the specific equations and their use in this version of the filter.
Figure 1-1. The ongoing discrete Kalman filter cycle. The time update projects the current state estimate ahead in time. The measurement update adjusts the projected estimate by an actual measurement at that time. Notice the resemblance to a predictor- corrector algorithm.The specific equations for the time and measurement updates are presented below in Table 1-1 and Table 1-2.
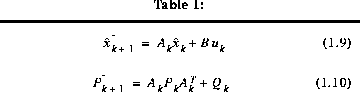
Again notice how the time update equations in Table 1-1 project the state and covariance estimates from time step k to step k+1.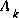 
and B are from (1.1), while 
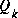is from (1.3). Initial conditions for the filter are discussed in the earlier references.
The first task during the measurement update is to compute the Kalman gain,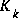 
. Notice that the equation given here as (1.11) is the same as (1.8). The next step is to actually measure the process to obtain 
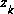, and then to generate an a posteriori state estimate by incorporating the measurement as in (1.12). Again (1.12) is simply (1.7) repeated here for completeness. The final step is to obtain an a posteriori error covariance estimate via (1.13).
After each time and measurement update pair, the process is repeated with the previous a posteriori estimates used to project or predict the new a priori estimates. This recursive nature is one of the very appealing features of the Kalman filter¯it makes practical implementations much more feasible than (for example) an implementation of a Weiner filter [Brown92] which is designed to operate on all of the data directly for each estimate. The Kalman filter instead recursively conditions the current estimate on all of the past measurements. Figure 1-2 below offers a complete picture of the operation of the filter, combining the high-level diagram of Figure 1-1 with the equations from Table 1-1 and Table 1-2.
Filter Parameters and Tuning
In the actual implementation of the filter, each of the measurement error covariance matrix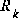 
and the process noise 
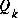(given by (1.4) and (1.3) respectively) might be measured prior to operation of the filter. In the case of the measurement error covariance 
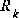in particular this makes sense¯because we need to be able to measure the process (while operating the filter) we should generally be able to take some off-line sample measurements in order to determine the variance of the measurement error.
In the case of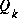 
, often times the choice is less deterministic. For example, this noise source is often used to represent the uncertainty in the process model (1.1). Sometimes a very poor model can be used simply by "injecting" enough uncertainty via the selection of 
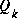. Certainly in this case one would hope that the measurements of the process would be reliable.
Figure 1-2. A complete picture of the operation of the Kalman filter, combining the high-level diagram of Figure 1-1 with the equations from Table 1-1 and Table 1-2.In closing I would point out that under conditions where
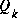and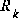 
.are constant, both the estimation error covariance 
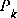and the Kalman gain 
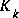will stabilize quickly and then remain constant (see the filter update equations in Figure 1-2). If this is the case, these parameters can be pre-computed by either running the filter off-line, or for example by solving (1.10) for the steady-state value of 
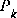by defining 
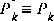and solving for 
.
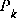It is frequently the case however that the measurement error (in particular) does not remain constant. For example, when sighting beacons in our optoelectronic tracker ceiling panels, the noise in measurements of nearby beacons will be smaller than that in far-away beacons. Also, the process noise
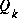is sometimes changed dynamically during filter operation in order to adjust to different dynamics. For example, in the case of tracking the head of a user of a 3D virtual environment we might reduce the magnitude of 
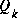if the user seems to be moving slowly, and increase the magnitude if the dynamics start changing rapidly. In such a case 
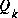can be used to model not only the uncertainty in the model, but also the uncertainty of the user's intentions.2 The Extended Kalman Filter (EKF)
The Process to be Estimated
As described above in section 1, the Kalman filter addresses the general problem of trying to estimate the state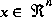 
of a first-order, discrete-time controlled process that is governed by a linear difference equation. But what happens if the process to be estimated and (or) the measurement relationship to the process is non-linear? Some of the most interesting and successful applications of Kalman filtering have been such situations. A Kalman filter that linearizes about the current mean and covariance is referred to as an extended Kalman filter or EKF.
In something akin to a Taylor series, we can linearize the estimation around the current estimate using the partial derivatives of the process and measurements functions to compute estimates even in the face of non-linear relationships. To do so, we must begin by modifying some of the material presented in section 1. Let us assume that our process again has a state vector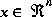 
, but that the process is now governed by the non-linear difference equation
(2.1)
with a measurement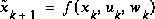 
,
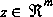that is (2.2)
Again the random variables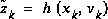 
.
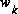and 
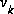represent the process and measurement noise as in (1.3) and (1.4).
In this case the non-linear function f(·) in the difference equation (2.1) relates the state at time step k to the state at step k+1. It includes as parameters any driving function uk and the process noise wk. The non-linear function h(·) in the measurement equation (2.2) now relates the state to the measurement zk.
The Computational Origins of the Filter
To estimate a process with non-linear difference and measurement relations, we begin by writing new governing equations that linearize an estimate about (2.1) and (2.2),
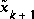and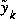 
are the projected state and measurement vectors from (2.1) and (2.2),
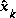is an a posteriori estimate of the state at step k,
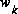and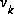 
represent the process and measurement noise as in (1.3) and (1.4).
,
,
,
.
,
.
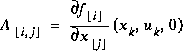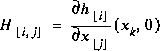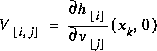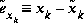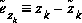(2.11)
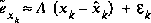, (2.12)
where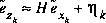 
,
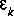and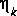 
are sets (ensembles) of independent random variables having zero mean and covariance matrices 
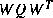and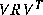 
.
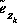in (2.10) and second (hypothetical) Kalman filter to estimate the prediction error 
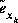given by (2.11). This estimate, call it 
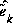, could then be used along with (2.9) to obtain the a posteriori state estimates for the non-linear process as
(2.13)
The random variables of (2.11) and (2.12) have approximately the following probability distributions (see the previous footnote):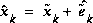
.
Given these approximations, the predicted value for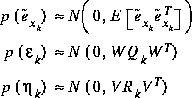 
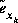is simply zero, and the Kalman filter equation used to estimate it is (2.14)
By substituting (2.14) back into (2.13) and making use of (2.10) we see that we do not actually need the second (hypothetical) Kalman filter: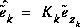
.
(2.15)
Equation (2.15) can now be used for the measurement update in the extended Kalman filter, with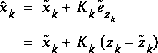 
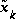and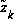 
coming from (2.1) and (2.2), and the Kalman gain 
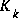coming from (1.11) with the appropriate substitution for the measurement error covariance. The complete set of EKF equations is shown below in Table 2-1 and Table 2-2.
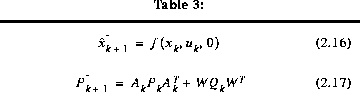
As with the basic discrete Kalman filter, the time update equations in Table 2-1 project the state and covariance estimates from time step k to step k+1. Again f(·) in (2.16) comes from (2.1),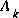 
and W are the Jacobians (2.5) and (2.6) at step k, and 
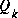is the process noise covariance (1.3) at step k.
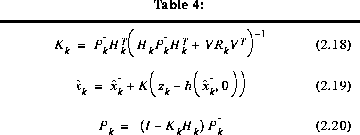
As with the basic discrete Kalman filter, the measurement update equations in Table 2-2 correct the state and covariance estimates with the measurement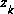 
. Again h(·) in (2.19) comes from (2.2), 
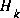and V are the Jacobians (2.7) and (2.8) at step k, and 
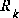is the measurement noise covariance (1.4) at step k.
The basic operation of the EKF is the same as the linear discrete Kalman filter as shown in Figure 1-1. Figure 2-1 below offers a complete picture of the operation of the EKF, combining the high-level diagram of Figure 1-1 with the equations from Table 2-1 and Table 2-2.
Figure 2-1. A complete picture of the operation of the extended Kalman filter, combining the high-level diagram of Figure 1-1 with the equations from Table 2-1 and Table 2-2.An important feature of the EKF, and indeed the key to the one-step-at-a-time approach, is that the Jacobian
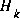in the equation for the Kalman gain 
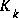serves to correctly propagate or "magnify" only the relevant component of the measurement information. For example, if there is not a one-to-one mapping between the measurement 
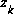and the state via h(·), the Jacobian 
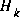affects the Kalman gain so that it only magnifies the portion of the residual 
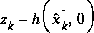that does affect the state. Of course if for all measurements there is not a one-to-one mapping between the measurement 
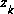and the state via h(·), then as you might expect the filter will quickly diverge. The control theory term to describe this situation is unobservable.
In this example, our process is governed by the linear difference equation
,
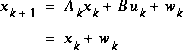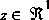that is
.
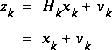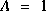. There is no control input so 
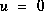. Our noisy measurement is of the state directly so 
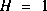. (Notice that I dropped the subscript k in several places because the respective parameters remain constant in our simple model.)
,
,
,
.
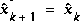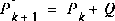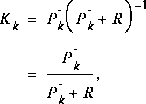
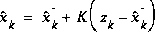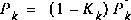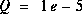. (We could certainly let 
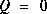but assuming a small but non-zero value gives us more flexibility in "tuning" the filter as I will demonstrate below.) Let's assume that from experience we know that the true value of the random constant has a standard normal probability distribution, so we will "seed" our filter with the guess that the constant is 0. In other words, before starting we let 
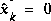.Similarly we need to choose an initial value for
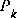, i.e. 
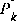. If we were absolutely certain that our initial state estimate 
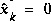was correct, we would let 
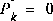. However given the uncertainty in our initial estimate 
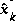, choosing 
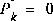would cause the filter to initially and always believe 
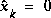. As it turns out, the alternative choice is not critical. We could choose almost any 
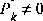and the filter would eventually converge. We'll start our filter with 
.
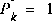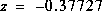(there is no "hat" on the z because it represents the "truth"). I then simulated 50 distinct measurements 
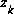that had error normally distributed around zero with a standard deviation of 0.1 (remember we presumed that the measurements are corrupted by a 0.1 volt RMS white measurement noise). I could have generated the individual measurements within the filter loop, but pre-generating the set of 50 measurements allowed me to run several simulations with the same exact measurements (i.e. same measurement noise) so that comparisons between simulations with different parameters would be more meaningful.In the first simulation I fixed the measurement variance at
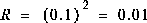. Because this is the "true" measurement error variance, we would expect the "best" performance in terms of balancing responsiveness and estimate variance. This will become more evident in the second and third simulation. Figure 3-1 depicts the results of this first simulation. The true value of the random constant 
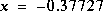is given by the solid line, the noisy measurements by the cross marks, and the filter estimate by the remaining curve.
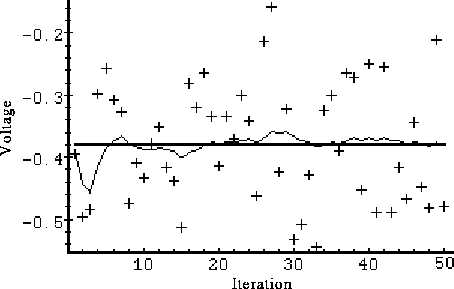
Figure 3-1. The first simulation:When considering the choice for. The true value of the random constant
is given by the solid line, the noisy measurements by the cross marks, and the filter estimate by the remaining curve.
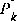above, I mentioned that the choice was not critical as long as 
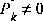because the filter would eventually converge. Below in Figure 3-2 I have plotted the value of 
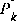versus the iteration. By the 50th iteration, it has settled from the initial (rough) choice of 1 to approximately 0.0002 (Volts2).
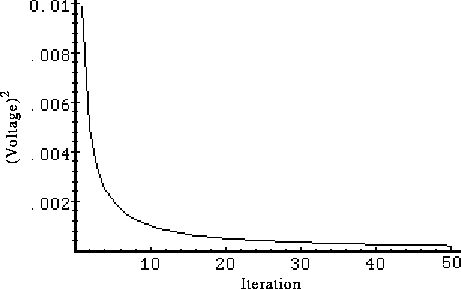
Figure 3-2. After 50 iterations, our initial (rough) error covarianceIn section 1 under the topic "Filter Parameters and Tuning" I briefly discussed changing or "tuning" the parameters Q and R to obtain different filter performance. In Figure 3-3 and Figure 3-4 below we can see what happens when R is increased or decreased by a factor of 100 respectively. In Figure 3-3 the filter was told that the measurement variance was 100 times greater (i.e.choice of 1 has settled to about 0.0002 (Volts2).
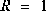) so it was "slower" to believe the measurements.
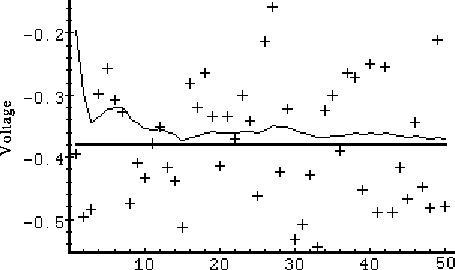
Figure 3-3. Second simulation:In Figure 3-4 the filter was told that the measurement variance was 100 times smaller (i.e.. The filter is slower to respond to the measurements, resulting in reduced estimate variance.
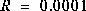) so it was very "quick" to believe the noisy measurements.
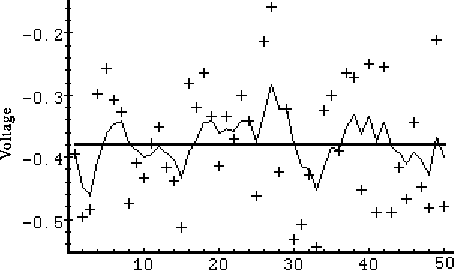
Figure 3-4. Third simulation:While the estimation of a constant is relatively straight-forward, it clearly demonstrates the workings of the Kalman filter. In Figure 3-3 in particular the Kalman "filtering" is evident as the estimate appears considerably smoother than the noisy measurements.. The filter responds to measurements quickly, increasing the estimate variance.
A Kalman Filter in Action: Estimating a Random Constant
Brown92 Brown, R. G. and P. Y. C. Hwang. 1992. Introduction to Random Signals
and Applied Kalman Filtering, Second Edition, John Wiley & Sons, Inc.
Gelb74 Gelb, A. 1974. Applied Optimal Estimation, MIT Press, Cambridge, MA.
Jacobs93 Jacobs, O. L. R. 1993. Introduction to Control Theory, 2nd Edition. Oxford
University Press.
Julier Julier, Simon and Jeffrey Uhlman. "A General Method of Approximating
Nonlinear Transformations of Probability Distributions," Robotics Research Group, Department of Engineering Science, University of Oxford
[cited 14 November 1995]. Available from http://phoebe.robots.ox.ac.uk/
reports/New_Fltr.zip (88K).
Kalman60 Kalman, R. E. 1960. "A New Approach to Linear Filtering and Prediction
Problems," Transaction of the ASME¯Journal of Basic Engineering,
pp. 35-45 (March 1960).
Lewis86 Lewis, Richard. 1986. Optimal Estimation with an Introduction to Stochastic Control Theory, John Wiley & Sons, Inc.
Maybeck79 Maybeck, Peter S. 1979. Stochastic Models, Estimation, and Control, Volume 1, Academic Press, Inc.
Sorenson70 Sorenson, H. W. 1970. "Least-Squares estimation: from Gauss to Kalman,"
IEEE Spectrum, vol. 7, pp. 63-68, July 1970.
and 
. The tuning is usually performed off-line, frequently with the help of another (distinct) Kalman filter.
,
.