Structural and Functional Connectomics
October 16, 2014
| Abstract |
These are preparatory thoughts and draft slides for a lecture on connectomics and functional circuit analysis in Bruno Olshausen’s Neural Computation (VS265) course at the University of California Berkeley on October 16, 2014. The early portion is dedicated to motivating students to devote a considerable part of their university education to learning the necessary foundational tools required to navigate in the rapidly evolving field of neuroscience. The latter part draws upon our collaboration with the Allen Institute for Brain Science focusing first on how the data is acquired and why it might be important to adapt existing or develop new tools to assist in data acquisition, and, second, on the challenges involved in learning models of the visual cortex from the mouse data collected by Clay Reid’s team at the Allen Institute.
Introduction: Some unsolicited recommendations
 |
Here are some subjects I would recommend that you master early in your education: differential, integral and multivariate calculus, probability theory including stochastic processes, statistics, ordinary and partial differential equations, linear algebra, graph theory and combinatorics. They’re all math you say? Whether you’re an experimentalist building tools to study the brain or a theorist trying to explain the data produced by such tools so as to construct models, math is essential to understanding the brain.
Mathematics provides a wide range of explanatory and predictive models, but you have to know how to apply those models to physical phenomena. How does a budding neuroscientist acquire such know-how if the field of neuroscience doesn’t offer a rich portfolio of mathematical models? The answer is that you don’t have to rely on neuroscience as your sole source of models. Physics is the best source of readily applicable models and there plenty of books featuring examples of how they are derived and applied [12].
And so I would add to the list of subjects worthy of study early in your education, physics and in particular classical physics including mechanics, optics, thermodynamics and electromagnetic theory. Mechanics may seem irrelevant given the scale of interactions we observe in the brain, but, mechanics is the subject in which the scientific method and the role of mathematical models are first explored, and so I suggest you bear with it and identify with Archimedes, Galileo and Newton.
Here’s a test of your basic understanding of electromagnetic theory, and, in particular, its role in reactions similar to those responsible for electrochemical signalling in the brain: Explain how a rechargeable Lithium battery works and why they can cause fires. Start with the simpler case of a copper-cathode and a zinc-anode and your choice of electrolyte, and then move on to the Lithium case. Make sure you can precisely state what it means for a current to flow in a given direction1. Give it a shot and then check your understanding here and here.
Quantum theory and optics play a role in such neurobiologically relevant technologies as optogenetics that makes it possible to excite and inhibit neurons with light and two-photon microscopy2 which when combined with genetically encoded calcium indicators (GECIs) such as CCaMP is the basis for calcium imaging. Here’s an example of a relatively simple question that an engineer or scientist might need to answer in the process of adapting or applying these technologies: What is the minimum frequency required for a photon to eject an electron from a magnesium surface?3
As shining examples of how far one can go in the field of neurobiology equipped with a physics background, Ed Boyden—the lead author on the original 2005 optogenetics paper [4] published in Nature—and Winfried Denk—the lead author on the 1990 paper [8] appearing in Science first describing two-photon fluorescence microscopy—were both trained as physicists. In addition to their considerable scientific achievements, both men have patented numerous inventions that have significantly advanced the field of neurobiology4.
Continuing with my recommendations for advancing your scientific careers, I suggest you sample from organic chemistry5, cellular and molecular biology, and the cognitive and social sciences to better understand how the scientific method is applied in the practice of different fields and to study additional examples of how to model physical and psychological phenomena. Taking a course on the history of science or reading a biography of Charles Darwin or William James will help you appreciate the challenges faced in confronting a subject when starting from a meager or misleading basis of understanding.
Ernest Rutherford, then Lord Rutherford, once said that ‘‘all science is either physics or stamp collecting’’, a statement that did not win him any friends in the many disciplines besides physics in which individuals who think of themselves as scientists ply their trade. However, the statement is misleading in its representation of science. In particular, it assumes a ‘‘one size fits all’’ characterization of what constitutes a scientific theory and how best to proceed in doing science.
Physics has a relatively simple ontology when compared with the biological sciences in which there are a lot of names used to categorize organisms, their constituent parts and the complex chemical reactions that govern their behavior. This state of affairs will likely get worse before it gets better, but be thankful that you have Google and Wikipedia to augment your memory, and become facile in using these and other analytical and information retrieval tools in your studies.
I’m overstating the much touted purity and elegant simplicity of physics. As it is often taught in college, there tend to be fewer terms to memorize and a deeper mathematical basis to fall back on when intuition fails us, but things are messier than they might seem from their presentation in textbooks. For example, many molecules of interest are formed by covalent bonds that depend on one sort of electron sharing, but you soon learn that there are other common molecules, like table salt and sulphuric acid, that consist of atoms held together by ionic bonds.
Moreover, unless you read your textbook carefully, you might miss out on the fact that a lot of molecules are held together by a combination of covalent and ionic bonds, and there other types of bonds, for example metallic and hydrogen bonds, that might not even appear in your introductory text. For a geologist or metallurgist, these simple basic types of bonds combine to give rise to an astounding diversity of materials with interesting and useful properties.
If you really want to commit some raw facts to memory, I suggest that you master the top few rows of the periodic table. You’ll probably never have to venture much beyond Osmium (Os) (#76) and you’ll be in pretty good shape if you only master Hydrogen (H) (#1) through Calcium (Ca) (#20). As an exercise, think about why the periodic table is different from, say, the modern version of the taxonomy developed by Carl Linnaeus, which is different from a list of the names of all the organs or bones in the human body.
Finally, despite how computer science is often perceived by other disciplines—primarily by those whose training predates the present era of ubiquitous computing, open-source software and the Internet, I maintain that an understanding of algorithms, machine learning, signal processing, computational complexity and programming is essential to the education of a modern neuroscientist. Relative to the other disciplines mentioned above, the importance of computer science will increase as the technologies for extracting information from the brain improve.
There are two reasons for the importance of computer science that we’ll explore in this lecture: (a) the amount of raw data required to understand many of the relevant phenomena in brain science defies direct human understanding unaided by computer analyses and the means for searching, sifting, factoring and fitting models, and (b) the complexity of the computations that give rise to cognitive phenomena is such that often the clearest explanation is an algorithm coupled with an implementation of the algorithm that simulates the phenomena of interest and thereby makes predictions that can be verified by experiment.
Explanations: Different principles dominate at different scales
Richard Feynman described how you might build half-scale versions of the sort of machine tools you would find in a well equipped machine shop, then use those machines to manufacture tiny half-scale versions of those, and so on down to the tiniest machines that could manipulate individual atoms and assemble complex molecules. It did not escape him that nature had already succeeded in this endeavor, albeit starting at the smallest and working its way up to the scale we are most familiar with.
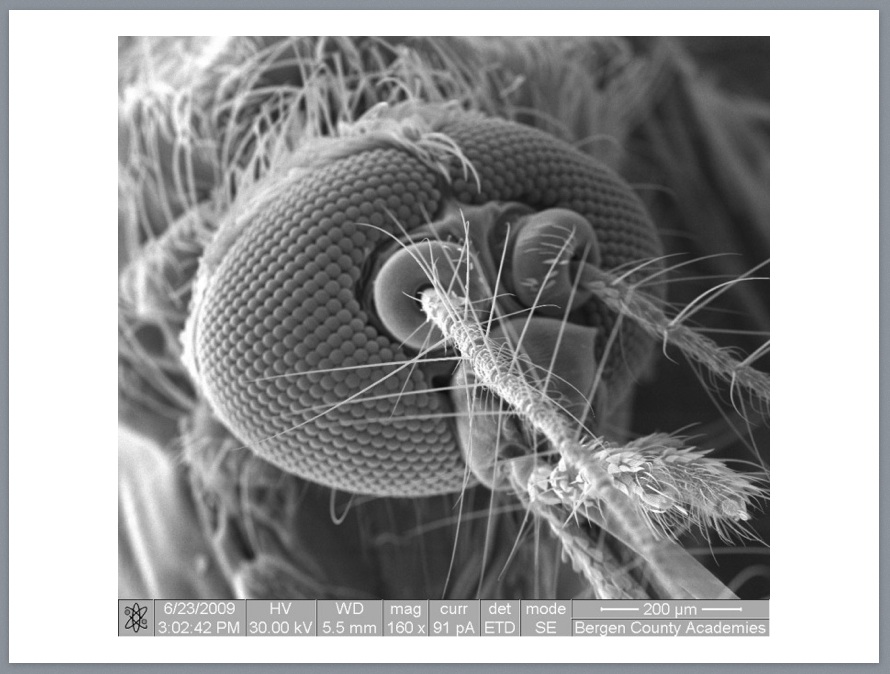
Feynman provided insights into the challenges faced by natural and man-made tiny machines, describing how, as you descend to smaller and smaller scales, different physical laws dominate. For example E. Coli use corkscrew-shaped flagella and molecule-sized motors to propel themselves through a watery fluid which is for them a viscous medium as thick as molasses. For organisms operating at millimeter scales, surface tension is an important consideration; at sub nanometer scales, Van der Waals force—the sum of the attractive / repulsive forces between molecules other than those due to covalent bonds—starts to play a key role.
 |
 |
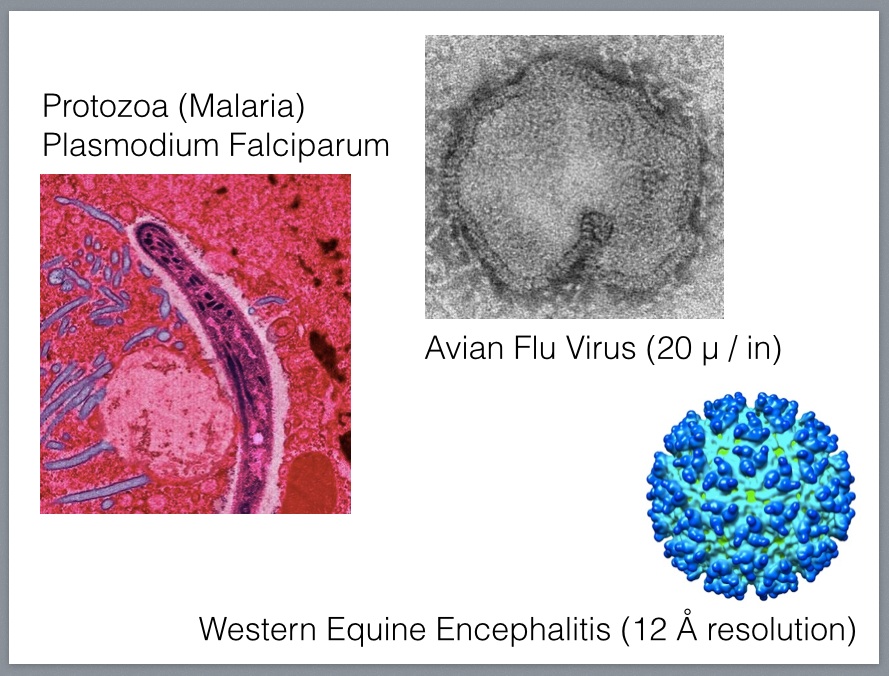 |
At this scale, the molecular machinery includes enzymes that enable reactions and complex molecules that assemble proteins and convert DNA into RNA (called RNA polymerase) and RNA into DNA (called DNA polymerase), one sort of which is called reverse transcriptase and is necessary in order for a virus to insert its genetic code into that of its host, thus making the host create many copies of the virus as a side effect of its normal cellular maintenance.
Our cells also perform quantum machinations on a routine basis. Rhodopsins found in our retinas and throughout nature convert photons into changes in membrane potential in a process called transduction that involves a cascade of electrical, chemical and even mechanical signals. Rhodopsins are the molecular basis for optogenetics. In this case, we are talking about interactions occurring at the scale of femtometers, and bioengineers and nanotechnologists building to tools for biologists to use at this scale have to think in terms of processes that play out in time measured as femtoseconds6.
The Experimentalists: Plus a couple of token theoreticians
 |
Faraday’s inventions including the electric motor (1821).
 |
Oliver Heaviside 1850-1950
Carl Friedrich Gauss 1777–1855
Maxwell’s equations as simplified by Heaviside (1861).
 |
Rutherford’s lab where he developed his atomic model (1911).
 |
Max Knoll 1897-1969
Early transmission electron microscope developed in (1931).
 |
Andrew Huxley 1917-2012
Equivalent circuit model for the Hogkin-Huxley model.
Equipment used in developing action-potential model (1952).
 |
Torsten Wiesel 1924-
Experimental apparatus to study the cat visual cortex (1959).
 |
Raymond Damadian 1936-
Early magnetic resonance device used in first human scan (1971).
 |
View down the 27km circular tunnel enclosing the LHC accelerator.
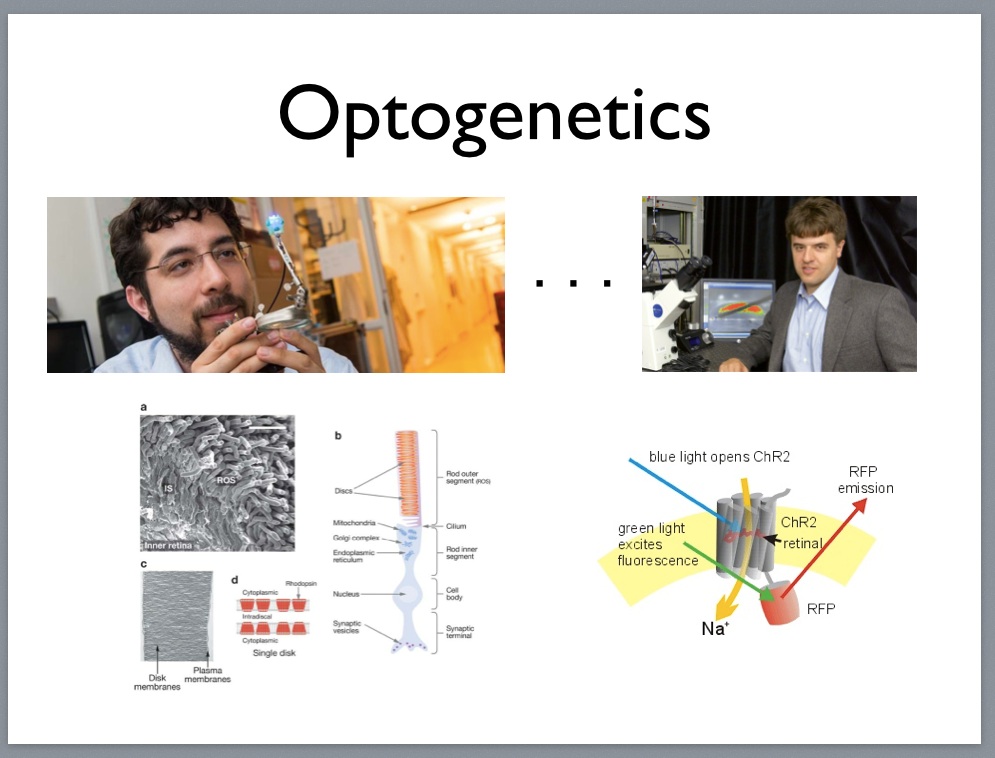 |
Karl Deisseroth 1971-
Rhodopsin in rod outer segment discs of the retina.
Channelrhodopsin optogenetic excitation and inhibition (2005).
Breaking the ‘‘Laws’’ of Physics: ‘‘No’’ is not an acceptable answer
I’ve yet to see an experimentalist who was satisfied with the technologies he or she could purchase off the shelf. They’ll often buy one off the shelf, e.g., an electron microscope from Zeiss or an fMRI machine from Siemens or GE, but it isn’t long before they have the cover off and are tinkering with the innards. Most experimentalists are wary of ‘‘laws’’ and ‘‘fundamental limits’’ as they often as not turn out to be misleading or flat out wrong. A good example is the diffraction limit for the resolution of visible light microscopy.7.
Conventional light microscopy resolution is inversely proportional to the wavelength of light used to illuminate the target and so light microscopy resolution is limited to a few hundred nanometers, e.g., visible-light microscope with high numerical aperture can achieve resolution of 250 nm. Super-resolution imaging beats the diffraction limit by either exploiting other physical principles, e.g., capturing the information in evanescent waves, or by using multiple images and computation to achieve sub-pixel resolution. For example, STORM — provide 20 nm in the lateral dimensions and 50 nm in the axial dimension, whereas LIMON — in biological applications offer 25 nm resolution in all three dimensions.
Mark Schnitzer and researchers in his lab at Stanford have built a miniature fluorescent microscope that can be surgically attached to the head of a mouse allowing the animal to move about freely while simultaneously recording from hundreds of neurons using calcium imaging8 (VIDEO). The 1.9 g camera offers a wide field of view compared with other technologies and introduces fewer motion artifacts than two-photon microscopy in awake, head-fixed mice responding to experimental stimuli.
In a related application of computational photography, a team led by Alipasha Vaziri and Ed Boyden [28] have demonstrated how to image the 302 neurons in an awake, behaving nematode—C. Elegans, the only organism for which we have a complete connectome [30]—using light-field microscopy in combination with 3-D deconvolution.
 |
For an excellent overview of the current state of the art in two-photon imaging and its application in studying synaptic plasticity, you might check out Karel Svoboda from HHMI Janelia describing the recent advances in optical imaging of individual synapses (VIDEO) and the application of these techniques to studying plasticity and signaling in single synapses (VIDEO).
In these lectures, you’ll also learn about a method of activating molecules such as glutamate that stimulate learning and signalling with light which is called photo activation or more commonly the shorter but less intuitive term uncaging referring to the technique of first inactivating (caging) the molecule you want to control by attaching an additional molecular group, and then subsequently activating (uncaging) the molecule with light using techniques similar to those used in optogenetics.
There are several types of electron microscope neuroscientsts can choose from for imaging biological targets. Here’s a quick summary of the different types of electron microscopes and their resolving power:
SEM — area square millimeters, depth of field millimeters, resolution of nanometers;
AFM — area 150 × 150 micrometers, depth of 10-20 micrometers, sub-nanometer resolution10;
STM — scanning tunneling — 0.1 nm lateral resolution and 0.01 nm depth resolution;
TEM — transmission electron — resolution of a few nanometers — area similar to SEM;
FIB — focused ion beam — resolution of 5 nm with the added benefit that the 3-D volume of the specimen can be examined without using a conventional microtome by precisely ablating top surface of the specimen thereby achieving higher resolution in the z-axis;
Scientists at HHMI Janelia Farm Campus have been experimenting with the FIB technologies. Clay Reid and his colleagues at Harvard modified their TEM to increase the field of view so it could be used for connectomics. As I describe in the lecture, their modifications involved a significant engineering effort. Here is a list of some of the scientists working at the forefront of micro-scale connectomics:
Davi Bock, HHMI Janelia Farm Campus
Winfried Denk, Max Planck, Tübingen
Josh Lichtman, Harvard University
Clay Reid, Allen Institute for Brain Science
Sebastian Seung, Princeton University
There is more to getting good electron micrographs than picking the right microscope. The tissue has to be carefully prepared in a process that involves several time-consuming steps and a number of chemicals many of which are very toxic. First the tissue is fixed using formaldehyde or other chemical fixatives to preserve the tissue from degradation, and maintain the structure of the cell and its sub-cellular components. Next it is dehydrated and the water replaced with a supporting matrix like paraffin or epoxy resins. Finally the tissue is stained, embedded in a block often of the same material used for the supporting matrix and mounted in the device used for thin sectioning. Here’s a manual describing protocols for preparing tissue samples for electron microscopy.
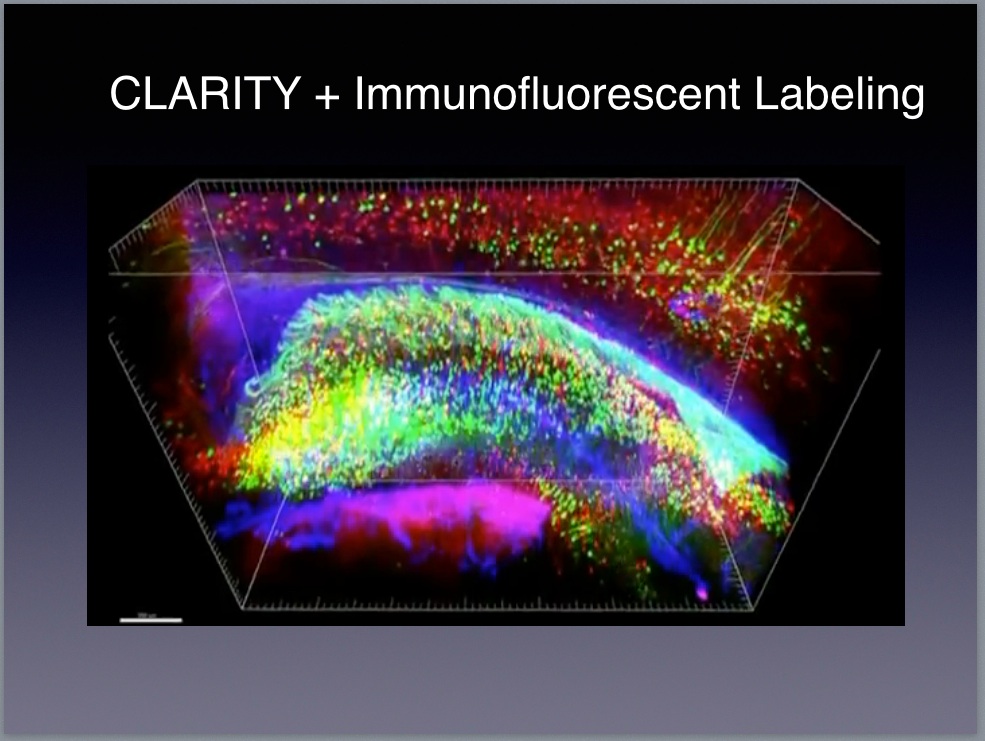 |
Many of the new technologies for probing the secrets of neural tissue don’t involve any hardware at all, but rather they exploit existing biological molecules, e.g., channelrhodopsins used in optogenetics, and whole organisms, e.g., retroviral gene delivery, or synthetic biological agents—see here for the announcement of a new PLoS (Public Library of Science) journal devoted to Neuroscience and Synthetic Biology. With the success of optogenetics and numerous examples from research on gene sequencing, e.g., the use of a thermostable polymerase found in T. aquaticus and applied in PCR (Polymerase Chain Reaction) to generate many copies of a gene, the search for biomolecules that can be used to encode, decode and transfer information.
Kording et al [18, 32] propose the idea of using a polymerase that has misincorporation rate—the probability that the polymerase will incorporate the wrong nucleotide at the location of a given base pair in a DNA sequence— is sensitive to the local concentration-density of calcium cations—positive calcium ions, Ca2+—to create a DNA ticker tape that could encode information about spiking neurons. Basically this polymerase would be expressed in neurons and spontaneously produce DNA records of neuronal activity that could be subsequently read off by gene-sequencing technology to recover spike chains.
In another proposal exploiting high-throughput gene sequencing technology, Zador et al [20, 31] propose a method of using a retrovirus to infer the connectome of living brains. The basic approach relies on the ability to genetically engineer cells capable of producing a DNA barcode in the form of a DNA sequence that would uniquely identify each cell. A retrovirus is then employed to transfer the cell’s barcode to each of its synapse-connected neighbors. All of the component technologies are currently possible and Zador’s lab at Cold Spring Harbor is working to assemble them into a reliable technology.
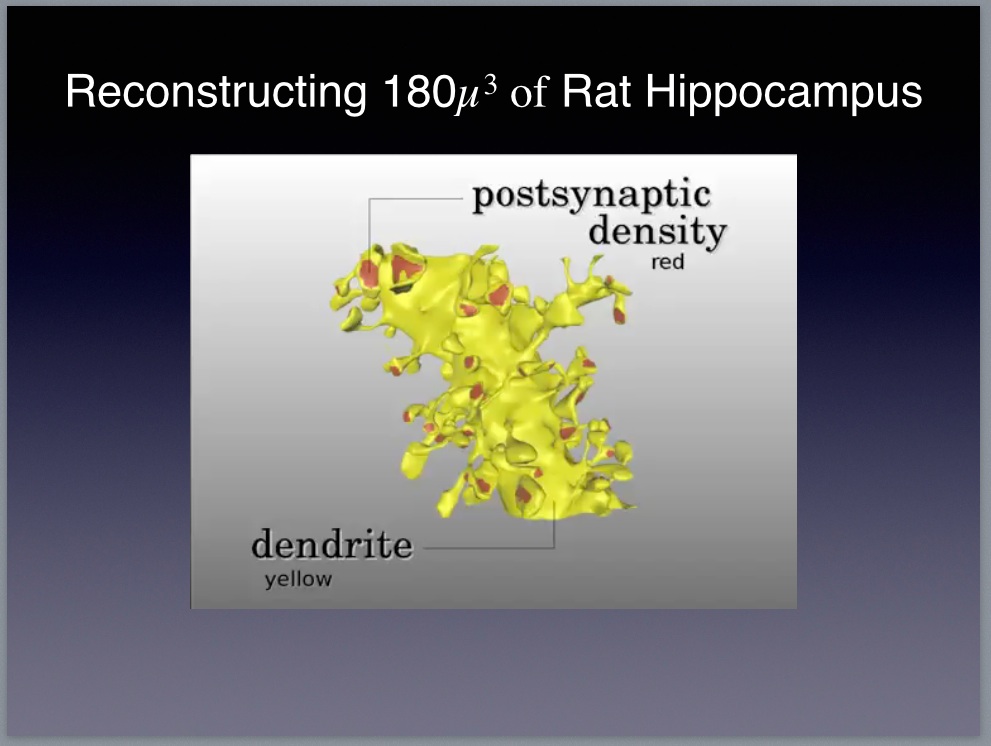 |
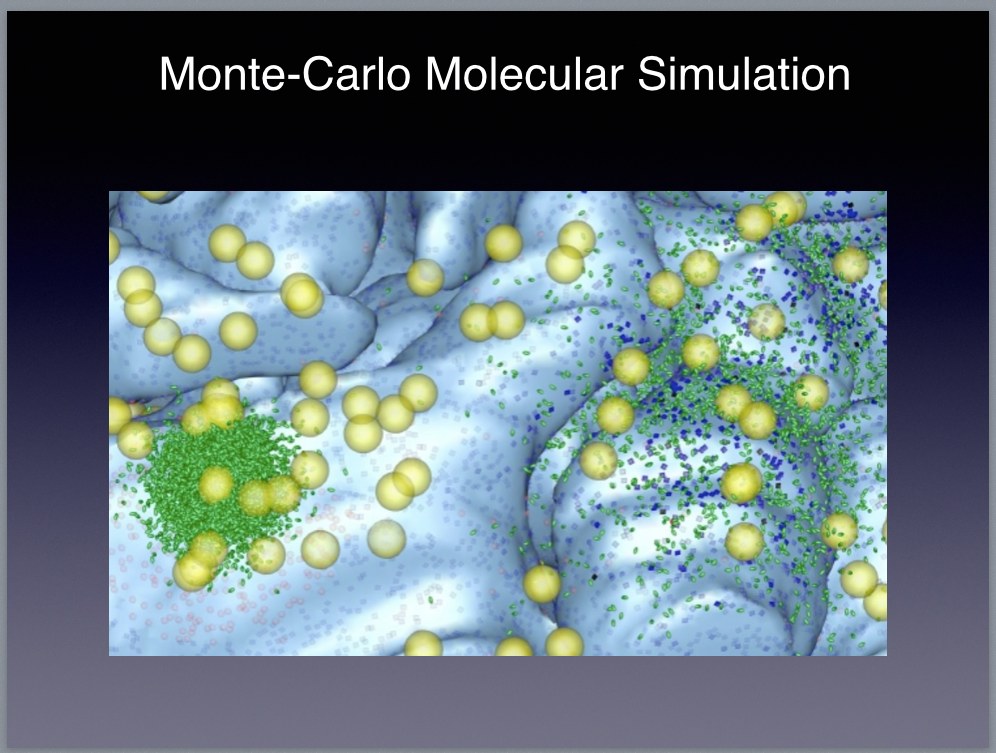
Kristen Harris from the University of Texas Austin
Daniel Keller from the É́cole Polytechnique Fédérale de Lausanne
This VIDEO from which the above image is taken shows a biologically-accurate model consisting of 450 synapses, 69 axons, and 77 dendritic spines. The model includes a complete—to the extent that we understand the relevant biology—account of the biophysics allowing researchers to set the initial conditions and the run a Monte-Carlo simulation of the neural circuitry. The simulation software11, called MCell, is able to reproduce the behavior of all the biologically active elements in the model including neurons and their associated neuropil, astrocytes that surround the neurons, and changes in the local field potentials in the extracellular matrix. Sejonowski and the rest of the team created the model to test a hypothesis about the role of astrocytes in neural computation. See the article on the HHMI website describing this research.
Functional Connectomics: What does that circuit compute?
Neuroscience has no shortage of models, but it’s a good bet that most of them aren’t very good at explaining what’s actually happening down at the level of circuits. I take that back; the Hodgkin-Huxley model does a good job of predicting how an isolated giant squid axon will respond to a change in its membrane potential. I’m being facetious; I think the H-H model is a wonderful achievement and it has had a significant impact on the field of neurobiology [1, 13]. But it doesn’t tell us very much about the behaviour of circuits composed of interconnected neurons, though there are plenty of scientists that would argue against that view.
Structural connectomics will tell us what those circuits look like, but alone it is like someone gave us the wiring diagram of a computer but didn’t tell us how resistors, capacitors, inductors, transistors and conducting and insulating materials work. Actually, we sort of know how an individual transistor—a neuron in our computer analogy—works if you believe H-H. Unfortunately, the analogy breaks down when you consider that the mammalian brain has hundreds if not thousands of different types of neurons that traffic in an equally daunting number of synaptic neurotransmitters and diffuse neuromodulators12 that propagate signals by a half-dozen or so pathways—chemical, electrical, genetic, diffusion, hormonal, mechanical.
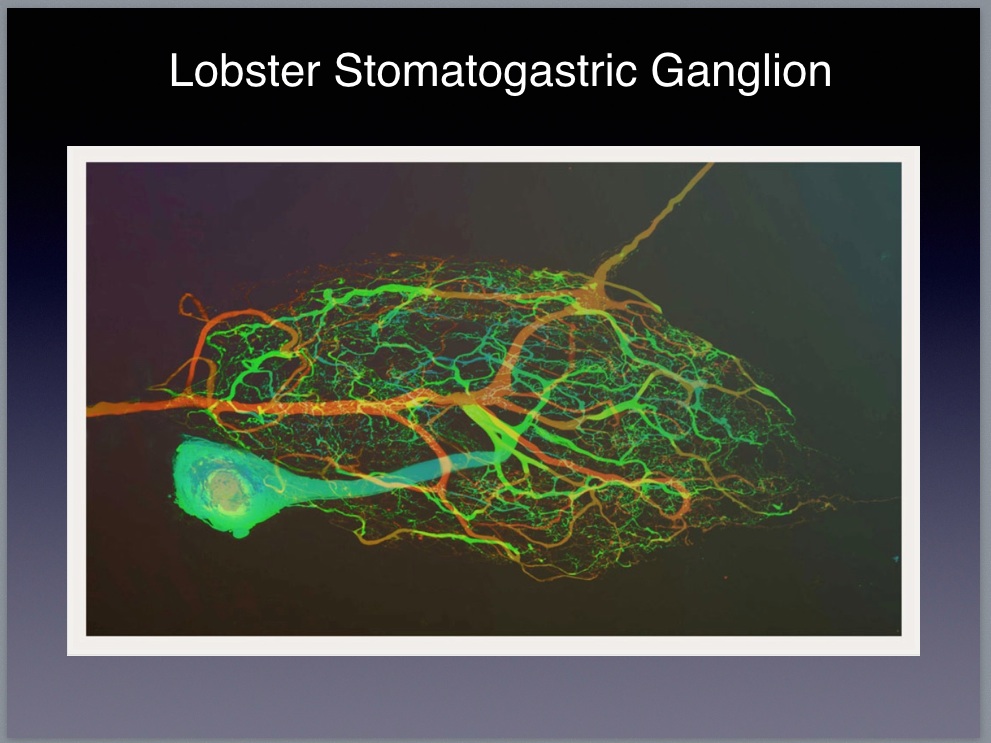 |
Will having more data really make a difference given the current state of knowledge? How much do we understand about, say, the neural circuitry responsible for bird song? Answer: Less than you might imagine, but we have made headway [9]. If birdbrains are hard to crack, why not work on something ‘‘really simple’’ like C. Elegans for which we already have the connectome for all 302 neurons? The OpenConnectome Project is a collection of scientists—including amateurs and professionals if that distinction even makes sense here—working to do just that. Unfortunately, the 302 neurons that comprise the C. Elegans nervous system consist of roughly 151 distinct types of neurons—the worm is bilaterally symmetric—that are spiking but not in the same way that mammalian neurons are spiking. By the way, someone asked if nematodes have neuromodulators. Apparently they do [10].
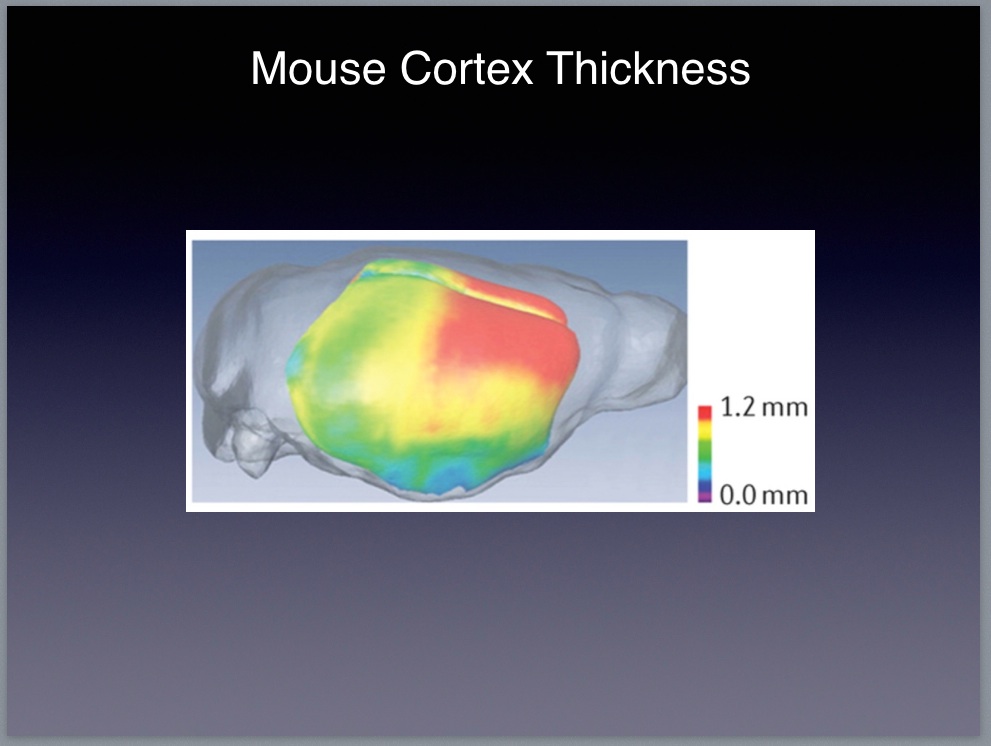 |
Let’s suppose we can identify the inputs and outputs by some means. We can easily create a neural network (NN) with a few billion tunable weights and assign the input neurites to NN input units and the output neurites to NN output units. Divide the data into training and testing, and then try this a few million times—sampling from the class of network topologies and weight distributions—and see how well the models can predict the behaviour of the circuit on the test set.
Suppose we’re lucky and we do a good job on the test data. What have we proved? How do you think such a result would be received by the neuroscience community. I was assuming that all of the data—training and test—was from a single organism, say a mouse. Suppose the data includes recordings from multiple mice—more than one and fewer than 100, and suppose for the sake of argument that we can do a pretty good job of extracting roughly the same circuit from each animal for some instantiation of ‘‘same.’’
Once again, suppose we’re lucky and our model generalizes across different mice. Now how do you think neuroscientists would react? Consider the recent run of papers claiming—at least according to the hyperbolic accounts in the popular press—to be able to ‘‘read minds’’ by analyzing fMRI scans [25, 26, 24, 16]. What do you think of the results reported in these papers? They do seem to show some generalization between individuals.
I’d like you to think about these questions and prepare a few of your own for class. Do you have a better way of tackling the problem of making sense of all the data we’re expecting from the technologies discussed above? Do you think the rest of the field has a good handle on how to proceed? If you were going to try to fit a model to the data, what family of models would you choose? In the few last paragraphs of this annotated version of the lecture, I’ll lay out a straw-man reductionist research program for you to critique and improve upon.
 |
I’m not convinced by Winfried’s argument, but, in any case, for now let’s continue with the modeling discussion. The basic idea is to build accurate models for each cell type using a detailed molecular modeling tool such as MCell or Neuron. To do so, we collect a subset of the calcium-imaging recordings containing representative instances of each cell type and fit a multi-compartmental Hodgkin-Huxley model to each subset. The resulting cell-type-specific models are likely to be our best bet in terms of accurately modeling the dynamics, but they will be very expensive computationally to simulate.
However, we can use the H-H model to train a simpler but computationally-tractable model such as a leaky-integrate-and-fire model of the sort that Izhikevich and Edelman [14] used in their large-scale simulations. Substituting the simpler but substantially faster models for the H-H models, we can then build a variant of the Izhikevich and Edelman model, but with a significantly more accurate model of the network than Izhikevich and Edelman in terms of cell-type-specific models for individual neurons, their connections and estimates of their synaptic strength.
The resulting complete model of the target tissue will have a number of additional global parameters that can be tuned using the calcium-imaging training data. This is obviously a very sketchy description, but you can probably get a pretty good idea of how things would play out. Suppose that this model accurately predicts the test data. Do you find it any more compelling as an explanatory model for cortical computations? What computational experiments would you suggest as additional tests of its adequacy?
References
1 Conventional current direction is defined as the flow of positive charges. This might seem backwards given that negatively-charged electrons would appear to the charge carrier, but it’s merely a convention adopted initially by Benjamin Franklin.
The labeling of one polarity of charge as ‘‘positive’’ and the other as ‘‘negative’’ is totally arbitrary. It could be done either way and everything would still work out the same. Franklin didn’t choose wrong; he just chose. Labeling protons as negative and electrons as positive wouldn’t change anything.
Electric current is a flow of electric charge. Charge can be positive (protons) or negative (electrons), and both types of charged particles can and do flow in electric circuits:
In metal wires, carbon resistors, and vacuum tubes, electric current consists of a flow of electrons.
In batteries, electrolytic capacitors, and neon lamps, current consists of a flow of ions, either positive or negative or both (flowing in opposite directions).
In hydrogen fuel cells and water ice, current consists of a flow of protons.
In semiconductors, the current consists of holes, which are not quite the same as an absence of electrons.
The Hall Effect can be used to show whether a charge carrier is positively charged and flowing in one direction, or negatively charged and flowing in the other.
If you considered only the electron flow as current, your calculations would be wrong. You need to consider the net flow of charge, no matter what the charge carriers. Conventional current abstracts away the different charge carriers and represents all of these different flows as a net flow of positive charge, simplifying circuit analysis.
Conventional current is not the opposite of electron current, so if they were defined to flow in the same direction, it would be even easier to confuse them and go through life misunderstanding what current is. Electron current is a subset of conventional current. Conventional current combines the effects of electron, ion, proton, and hole flows all into one number. Wikipedia agrees:
In other media, any stream of charged objects may constitute an electric current. To provide a definition of current that is independent of the type of charge carriers flowing, conventional current is defined to flow in the same direction as positive charges.
2 Calcium imaging is one of the most powerful new technologies for recording from large numbers of neurons, in many cases in awake behaving animals. Calcium indicators serve as fluorescent markers to identify neural activity:
Calcium imaging techniques take advantage of so-called calcium indicators, fluorescent molecules that can respond to the binding of Ca2+ ions by changing their fluorescence properties. Genetically encoded indicators are fluorescent proteins derived from green fluorescent protein (GFP) or its variants (e.g. circularly permuted GFP, YFP, CFP), fused with calmodulin (CaM) and the M13 domain of the myosin light chain kinase, which is able to bind CaM. Genetically encoded indicators do not need to be loaded onto cells, instead the genes encoding for these proteins can be easily transfected to cell lines. It is also possible to create transgenic animals expressing the dye in all cells or selectively in certain cellular subtypes. Examples include Pericams, Cameleons and GCaMP. (SOURCE)
3 Assume that the photoelectric work function (energy threshold) for magnesium is 5.9 * 10−19 J (Joules). Question: What is the minimum frequency required for a photon to eject an electron from a magnesium surface? Answer: E = hf ; f = E/h = 5.9E-19 J / 6.63E-34 J s = 8.9E14 ; E = hc/w = 6.63E-34Js x 3E8 m/s / 475E-9 m = 4.19E-19 J. Given this analysis one might ask: Would a photon of blue light (475 nm) be able to eject an electron from a magnesium surface? Answer: No. The energy of the blue photon is less than the energy required to eject an electron from Mg.
4 Winfried was trained as a physicist at Cornell University, pioneered several key technologies now widely used in neurobiology, and is currently the Director of the Electrons — Photons — Neurons Laboratory at the Max Planck Institute for Neurobiology in Martinsried, Germany near Munich. In addition to two-photon microscopy (US Patent US5034613) he also invented the technology for automatically acquiring 3-D volumetric imagery at resolutions of a few nanometers known as Serial Block-Face Scanning Electron Microscopy (US patent US8431896). Ed has degrees in Physics and Computer Science (the title of his undergraduate thesis was ‘‘Quantum Computation: Theory and Implementation’’) and received his PhD (‘‘Task-specific neural mechanisms of memory encoding’’) in Neuroscience from Stanford University. In addition to his work on developing tools for the optical control of cells (US Patent WO2013071231A1), his lab is developing radically new methods for extending light microscopy and robotically scaling neurophysiology. He is currently the leader of the Synthetic Neurobiology Group in the MIT Media Lab, a principle investigator at the McGovern Institute and Co-Director of the MIT Center for Neurobiological Engineering.
5 With the recent press concerning postmortem tissue preparation techniques that render biological samples transparent [6, 19], biochemists with expertise in polymer chemistry including knowledge of synthetic and biological macromolecules are now in demand in neurobiology labs. To paraphrase a line from The Graduate in which Benjamin, played by Dustin Hoffman, feeling out of place at a cocktail party is offered some friendly investment advice by the irritatingly convivial Mr. McGuire played by Walter Brooke:
Mr. McGuire: I just want to say one word to you. Just one word.
Benjamin: Yes, sir.
Mr. McGuire: Are you listening?
Benjamin: Yes, I am.
Mr. McGuire: Polymers.
Benjamin: Exactly how do you mean?
6 Electrons and protons are attracted to each other by electromagnetic forces between their opposite charges. Internally protons are held together by the strong nuclear force and weak interaction in radioactive atoms with nuclei too large for the strong force to bind their constituent particles together. Electrons are fundamental particles and therefore can’t fall apart. They can and routinely do shift around and it is this shifting about—jumping from one electron shell to another of higher energy and visa versa—that is responsible for the photoelectric effect.
7 As I was writing these notes, the latest (print) issue of The Economist arrived in the mail with a story about the 1914 Nobel Prize winners. This year there were three awards made for circumventing the diffraction limit:
The chemistry prize went to Eric Betzig, Stefan Hell and William Moerner, for inventing ways to make microscopes better, by circumventing what is known as Abbe’s resolution limit. This is the fact, noted in 1873 by Ernst Abbe, that a microscope cannot properly see any object smaller than half the wavelength of the light it uses.Dr Hell, of the Max Planck Institute for Biophysical Chemistry, in Germany, relied on lasers to circumvent the resolution limit. By delivering precisely calibrated pulses, a laser can be used to make certain molecules fluoresce. His system employs two beams, one to induce fluorescence and another to suppress it in all but a tiny area of the sample being studied. By sweeping the combined beam across a sample, and measuring the light emitted by the glowing molecules, features much smaller than the Abbe limit can be resolved.
Dr Betzig, of the Howard Hughes Medical Institute, and Dr Moerner, of Stanford University, also rely on fluorescence. In their technique, a biological sample is tagged with a special protein that glows when exposed to light. Weak light of the appropriate wavelength is shone on the sample, which persuades a small fraction of the special protein molecules to light up. An image is taken, the light is switched off, and the procedure is repeated. Provided the glowing molecules are farther apart than the Abbe limit, their relative positions can be discerned. Repeat the procedure and a different set of molecules will glow. Repeat it often enough, and combining the images it generates allows a detailed picture that includes features smaller than the Abbe limit to be built up. (SOURCE)
8 Here’s the clearest and most succinct characterization I could find describing the role of calcium—both pre- and post-synaptic neurons—in synaptic signal transduction. I’ve included the entire post and provided a link to the source page at the end. It is common in many textbooks to emphasize calcium’s role in the presynaptic neuron. The connection to NMDA receptors on the postsynaptic neuron often gets overlooked or forgotten. Hopefully armed with this explanation you can extend your search to learn more about calcium’s role in memory, but here we are primarily concerned with explaining how calcium imaging works:
In a classic synapse, calcium’s main role is to trigger the release of chemicals (called neurotransmitters) from the presynaptic neuron. How calcium does this is well established and is achieved through voltage-gated calcium channels located on the membrane of the presynaptic terminal. These channels open in response to membrane depolarization, the type of signal carried by an action potential.Calcium imaging works by introducing a molecule called a calcium indicator into the cell either by injecting it or by genetically modifying the organism so that its cells express the indicator at a fixed rate. The calcium indicator combines a fluorescent molecule along with a second molecule that changes its conformation when bound to a calcium ion.The whole process goes something like this: When an action potential arrives at the presynaptic terminal, it depolarizes the membrane sufficiently to open voltage-gated calcium channels. The calcium gradient across the membrane is such that when these channels open, an inward calcium current is produced, with calcium rapidly entering the cell. Calcium is rapidly bound by a presynaptic intracellular protein called synaptotagmin. Synaptotagmin is considered a calcium sensor that triggers a host of downstream events. Ultimately, synaptotagmin activation results in the fusion of neurotransmitter vesicles with the presynaptic membrane. These vesicles fuse with the membrane through interactions between v- and t-snares (the ‘‘v’’ and ‘‘t’’ stand for ‘‘vesicular’’ and ‘‘target’’, respectively) causing the release of neurotransmitters into the space between the pre- and postsynaptic terminal. Individual molecules of neurotransmitter diffuse across this space, called the synaptic cleft, and ultimately bind to receptors on the postsynaptic cell membrane.
Since calcium triggers the conversion of an electrical signal (the action potential) into a chemical one (the release of neurotransmitters), calcium can be thought of as the trigger for electrochemical transduction (the term literally means the conversion of electrical into chemical information).
Note that calcium’s role is not limited to the presynaptic terminal; plenty of other synaptic phenomena rely on calcium. For example, at the specialized synapses between neurons and muscle cells (called the neuromuscular junction), binding of the neurotransmitter acetylcholine to the muscle cell triggers a rise in calcium within the muscle cell, which ultimately leads to muscle contraction. Another example occurs in the brain and involves a postsynaptic receptor called the NMDA receptor. Activation of this receptor also produces a rise in intracellular calcium in the postsynaptic cell which contributes to a number of interesting phenomena, notably learning and memory. (SOURCE)
A molecule is said to be fluorescent if it absorbs light at a different wavelength than it emits light. If you shine one color light at a fluorophore, it will emit a different color, usually with a longer wavelength. The specific wavelengths at which a fluorophore absorbs and emits light are highly sensitive to the molecule’s structure. Because molecules often undergo conformational changes when they bind to another chemical, this binding event also has the potential to change the properties of the fluorophore. (SOURCE)Assuming that the pre-synaptic axon terminal—also called a synaptic bouton from the French word for ‘‘button’’—is populated with calcium indicators, when the bouton depolarizes in response to an action potential the in-rushing calcium ions bind with the calcium indicators resulting in a change in the wavelength of their emitted photons—a change that can be detected by a confocal or other suitable microscope equipped with appropriate signal-processing hardware.
The exact timing of this change with respect to membrane depolarization and subsequent signal transduction can be adjusted by tuning the molecular structure of the calcium indicator, and each generation of the GCaMP indicator has improved upon the previous so, that the current generation can detect a single action potential thereby demonstrating a dramatic improvement in spatial and temporal resolution [5, 29, 15].
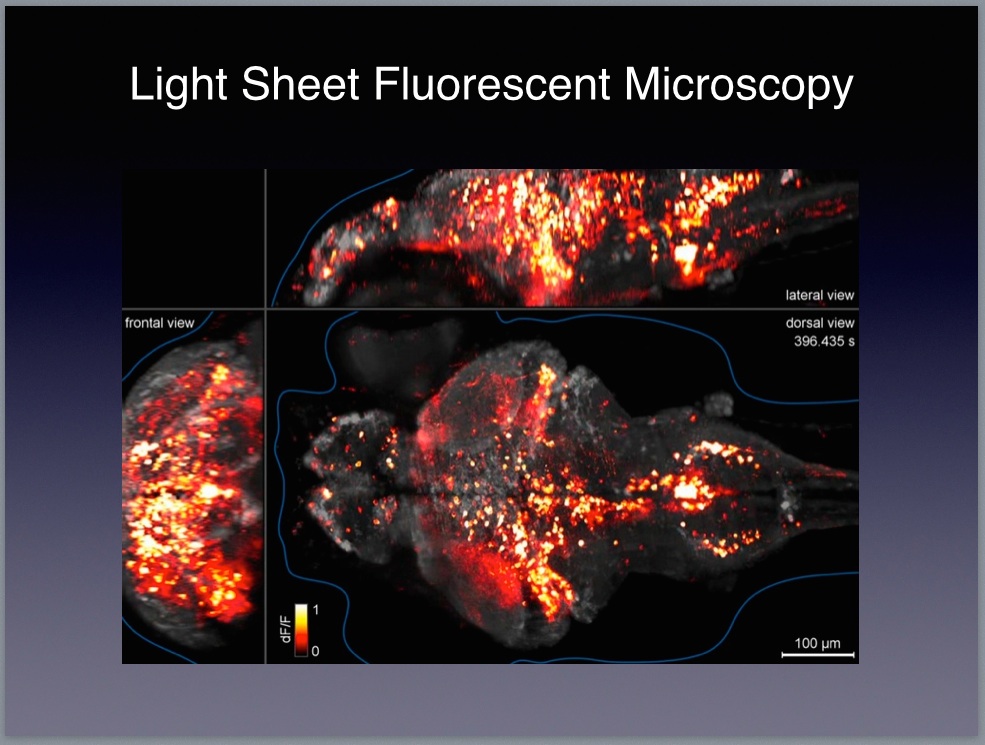
9 The Janelia website includes lots of resources for looking deeper into the relevant science and technology. In particular, you might want to check out videos by Karel Svoboda and Jason Kerr both of whom are investigators working at the Janelia campus. Here’s the description of the zebrafish work on the HHMI website:
Brain function relies on communication between large populations of neurons across multiple brain areas, a full understanding of which would require knowledge of the time-varying activity of all neurons in the central nervous system. Here we use light-sheet microscopy to record activity, reported through the genetically encoded calcium indicator GCaMP5G, from the entire volume of the brain of the larval zebrafish in vivo at 0.8 Hz, capturing more than 80% of all neurons at single-cell resolution. Demonstrating how this technique can be used to reveal functionally defined circuits across the brain, we identify two populations of neurons with correlated activity patterns. One circuit consists of hindbrain neurons functionally coupled to spinal cord neuropil. The other consists of an anatomically symmetric population in the anterior hindbrain, with activity in the left and right halves oscillating in antiphase, on a timescale of 20 s, and coupled to equally slow oscillations in the inferior olive. (SOURCE)
10 Good is considered to be 0.1 nm lateral resolution and 0.01 nm depth resolution.
11 MCell and Neuron are simulators designed to simulate the dynamics of individual and circuit of neurons and their associated extracellular environment:
MCell is a modeling tool for realistic simulation of cellular signaling in the complex 3-D subcellular microenvironment in and around living cells—what we call cellular microphysiology. At such small subcellular scales the familiar macroscopic concept of concentration is not useful and stochastic behavior dominates. MCell uses highly optimized Monte Carlo algorithms to track the stochastic behavior of discrete molecules in space and time as they diffuse and interact with other discrete effector molecules (e.g. ion channels, enzymes, transporters) heterogeneously distributed within the 3-D geometry of the subcellular environment. (SOURCE)
12 Neuromodulators enable one-to-many and many-to-many neural signaling. Their general role as modulator has been known for some time, but in recent years much more attention has been given to understanding how diffuse neuromodulation and synaptic transmission work together to determine the function of neural circuits:
In neuroscience, neuromodulation is the process in which several classes of neurotransmitters in the nervous system regulate diverse populations of neurons (one neuron uses different neurotransmitters to connect to several neurons). As opposed to direct synaptic transmission, in which one presynaptic neuron directly influences a postsynaptic partner (one neuron reaching one other neuron), neuromodulatory transmitters secreted by a small group of neurons diffuse through large areas of the nervous system, having an effect on multiple neurons. Examples of neuromodulators include dopamine, serotonin, acetylcholine, histamine and others.A neuromodulator is a relatively new concept in the field, and it can be conceptualized as a neurotransmitter that is not reabsorbed by the pre-synaptic neuron or broken down into a metabolite. Such neuromodulators end up spending a significant amount of time in the CSF (cerebrospinal fluid), influencing (or modulating) the overall activity level of the brain. For this reason, some neurotransmitters are also considered as neuromodulators. Examples of neuromodulators in this category are serotonin and acetylcholine. (SOURCE)
13 Ephaptic coupling is similar in some respects to diffuse neuromodulation but more local within a collection of neurons and generally trafficking in the same neurotransmitters employed by the neurons in said collection in their more traditional cell-to-cell synaptic transmission:
Ephaptic coupling is a form of communication within the nervous system and is distinct from direct communication systems like electrical synapses and chemical synapses. It may refer to the coupling of adjacent (touching) nerve fibers caused by the exchange of ions between the cells, or it may refer to coupling of nerve fibers as a result of local electric fields.[1] In either case ephaptic coupling can influence the synchronization and timing of action potential firing in neurons. Myelination is thought to inhibit ephaptic interactions. (SOURCE)
14 Ectopic neurotransmission is the term scientists at the Salk Institute use to describe the release of neurotransmitters outside of synapses. A team of neuroscientists at the Salk led by Terry Sejnowski used a molecular model to simulate a neural circuit with and without accounting for ectopic neural transmission.
[They] created a highly accurate computer model simulation of the giant chick embryo synapse that connects nerve fibers originating in the brain with the neuron that controls the size of the pupil and the shape of the eye lens. This particular synapse is a favorite model for the study of synaptic transmission since the neurons forming what is known as the ciliary ganglion are rather simple, easily accessible and nerve impulses can be recorded from either the presynaptic or the postsynaptic element or both.Such recordings of nerve signals tipped off the researchers to the possibility that receptors outside of the synapse were routinely activated. But where did the necessary neurotransmitter molecules come from? Coggan and Bartol then simulated the release of neurotransmitter from single vesicles located within synapses as well as from vesicles located outside traditional synaptic junctions in what they called "ectopic release". Next they compared their predictions with actual recordings from living cells. ‘‘We could only match the physiological results when we allowed 90 per cent of the release to occur outside of synapses,’’ (SOURCE)
15 Here’s an estimate of the size of the image data resulting from a serial-section EM scan of a one-millimeter-cube of brain tissue:
If one were to reconstruct by EM all the synaptic circuitry in 1 cubic mm of brain (roughly what might fit on the head of a pin), one would need a set of serial images spanning a millimeter in depth. Unambiguously resolving all the axonal and dendritic branches would require sectioning at probably no more than 30 nm. Thus the 1 mm depth would require 33,000 images. Each image should have at least 10 nm lateral resolution to discern all the vesicles (the source of the neurotransmitters) and synapse types. A square-millimeter image at 5 nm resolution is an image that has 4 × 1010 pixels, or 10 to 20 gigapixels. So the image data in 1 cubic mm will be in the range of 1 petabyte (250 1,000,000,000,000,000 bytes). The human brain contains nearly 1 million cubic mm of neural tissue. — From Discovering the Wiring Diagram of the Brain by Jeff W. Lichtman, Clay Reid, Hanspeter Pfister, Harvard University and Michael F. Cohen, Microsoft Research