Sensors are typically noisy and the information they provide is often ambiguous or misleading. A robot rolling down a corridor delivering mail is likely to be uncertain about the distance to the walls on either side of it; the robot can only guess whether it is approaching a turn in the corridor or there are people standing around the water cooler blocking the corridor. Figuring out when and how to resolve uncertainty is an important part of robotics and automated control more generally. Given that the language of probability and statistics is often used to describe the state of a robot's knowledge about the world, it's not too surprising that these areas of mathematics play an important role in robotics.
In a single lecture it would be impossible to do justice to the many techniques used in robotics for reasoning under uncertainty. Instead I'll describe an example technique that illustrates some of the general ideas in the field and provides a practical foundation for building maps, localizing robots and planning paths for navigation purposes. We begin by developing a simple model for the ultrasonic sensor that we looked at in the previous lecture. The method we'll be talking about was originally developed for a relatively simple robot; however, it requires considerable computational overhead, both in terms of time and storage, and hence it is not appropriate for a Lego robot unless you care to perform the calculations and store the map on a remote computer.
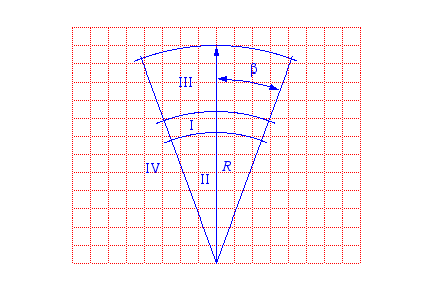
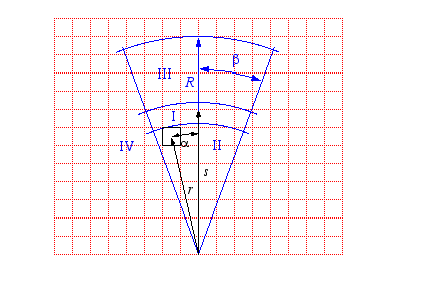
You'll recall from our experiments that the ultrasonic sensor has both a minimum and a maximum range and the beam of acoustic energy spreads in a cone of approximately 30 degrees. If the sensor returns a value that is between the minimum and the maximum and we assume that the nearest object has the right surface characteristics, then the returned value is proportional to the distance to this object with a perhaps a little error. There is additional error along the arc perpendicular to the sensor axis. We don't know the angle between the sensor axis and the nearest point on the object; all we know is that it is probably within the 30-degree cone. The diagram below shows the basic sensor model.

The area in front of the sensor is divided into four areas labeled I, II, III and IV. These four areas are superimposed over a grid of cells. Each cell is meant to represent a region of physical space. The grid will be used as a data structure to record what we know about physical space. Our objective is to keep track for each cell the probability that the cell is occupied and therefore constitutes an obstacle to the robot. This data structure is typically called an occupancy grid. In the graphic above, the occupancy grid is in two dimensions and obstacles are assumed to project out of the floor. It is conceptually straightforward to generalize to three-dimensional occupancy grids.
The area labeled I is meant to indicate, for a given sensor value, the cells in which the nearest point on the nearest object is likely to be found. The area labeled II indicates cells that are likely not to be occupied as otherwise the surfaces of the objects in those cells would have reflected the sonar ping and the returned value would have been less. Finally, areas III and IV correspond to cells that the current sensor reading do not tell us anything about. The greek letter β indicates half the angle of the cone. The trick is to provide a method of updating cells as the robot moves about and takes sonar readings and update the occupancy grid to reflect all of the sensor information that the robot has gathered. The grid then provides a basis, or map, for navigation.
In the following, I'll assume very basic knowledge of probability. Let the variable C denote the proposition (event) that a particular cell is occupied; a bar over a variable indicates its complement, namely that the cell is empty. Let Pr(C) denote the probability that C is occupied. Let r and α denote, respectively, the distance and angle to C.
The following simple model for region I captures the idea that the sensor is more accurate the closer the cell is to the sensor (small r) and the closer it is to the axis of the sensor (α). We assume that a cell is never occupied with probability one and hence we multiply the first term by the factor M which is a probability less than one.
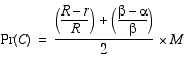
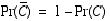
The model for region II is similar to the model for region I except that the probabilities are reversed since the sensor reading is providing evidence that cells in this region are empty. Unlike region I we allow cells in region II to be empty with probability one.
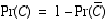
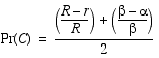
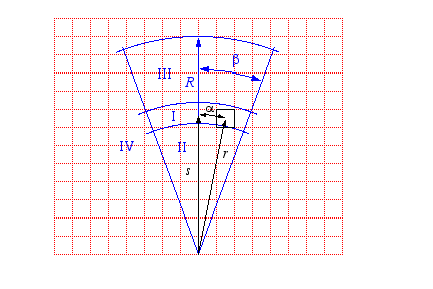
Here is a graphic showing the parameters for two cells, one in region I and a second in region II, from a particular reading. The robot would have to identify and update each of the cells in regions I and II. There's a further complication that we'll return to later, namely, that if the robot moved since it's last sensor reading and there may be uncertainty in its new location with respect to its old location. In this case, the robot should update all of the cells in its grid taking into acount the increase in uncertainty due to the uncertain movement. But, for the time being let's assume that the robot's movements and location updates are error free.
|
|
Here's the sensor model instantiated for the case above and to the right in which r is 6, α is 5 and M is 0.98.
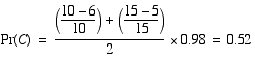
Using the axioms of probability and the fact that C and its complement are mutually exclusive and exhaustive alternatives, we can compute the probability of the complement easily.
More accurately, we should write Pr(C) as a conditional probability, Pr(si|C), the probability that the sensor would return the observed reading given that the cell is occupied. What we're really interested in however is the conditional probability Pr(C|,s1, s1,...,sn), i.e., the probability of a cell being occupied given a sequence of sensor readings. (Note the difference between the conditional probability of lung cancer given heavy smoking versus the conditional probability of heavy smoking given lung cancer. What do you think; are these two probabilities the same or different and, if different, in what way are they different?) Unfortunately, all we have is Pr(si|C) and (the real) Pr(C), the prior probability that the cell is occupied. Bayes rule provides us with the machinery we need. In the following, H denotes a (boolean) hypothesis and d represents the evidence or data. Bayes rule can be proven easily just using the definition of conditional probability: Pr(A|B) = Pr(A,B) / Pr(B).
Substituting for H and d, we obtain the following equation.
And, generalizing to the case of multiple sensor readings, we get a version of Bayes rule that enables us to compute the probability that we seek.
Using the axioms of probability and the notion of conditional independence, you can derive the following recursive update form of Bayes rule.
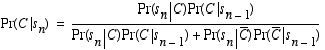
Now consider that the robot obtains two sensor readings some distance apart and let's look at how we update one particular cell that lies in region I of both instantiations of the sensor model.
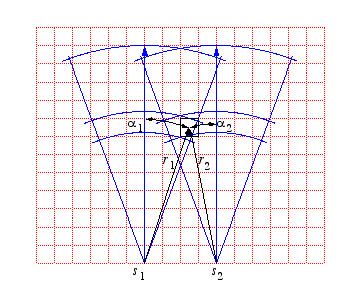
We'll assume that the first sensor readings is the first ever and hence our prior is completely unbiased.
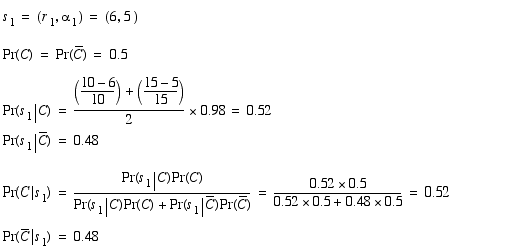
That Pr(s1|C) is equal to Pr(C|s1) is due to the 0.5 prior. Now Pr(C|s1) becomes the prior and the second sensor reading is incorporated as follows.
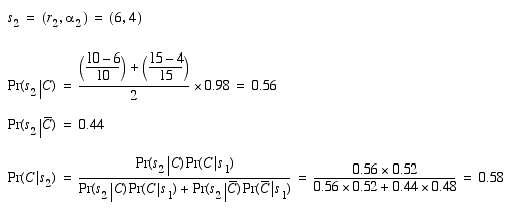
So now it should be clear that if we know the robot's position with respect to the coordinate system of the occupancy grid we can update the map for each sensor reading and the map will be accurate if the underlying assumptions are satisfied. So, what are the underlying assumptions? Well, for one, we assume that the surfaces of the objects in the robot's environment are diffuse in the sense that they reflect acoustic energy equally in all directions and enough energy is directed back toward the receiver on the sonar to stop the time-of-flight timer. Of course, this assumption is false! No real objects satisfy this requirement and many objects are significantly specular and may deflect the lion's share of the energy away from the sonar. This is true even with walls of painted wall board if the angle that the wall makes with the axis through the sensor is less than about 35 degrees. What could we do to avoid the mistakes that arise from this assumption about diffuse surfaces failing?
Another assumption that we make in updating the occupancy grid is that any pair of sensor readings is independent. What do we mean by this? What if you took two readings from the same sensor standing in the same spot? How would you combine the information in these two readings? Think about the sensor model. What if the cone was infinitesimally narrow? Now the error is only along the sensor axis. What is the model for the sensor in this case? Now think about the specular/diffuse assumption as it pertains to sensor error. What if we were sure that the surface of the object in front of the robot was diffuse, i.e., it satisfies are assumptions? All these questions illustrate the complications of coming up with a good model?
In the remainder of the lecture, we return to the problem of representing errors in movement, map registration, topological maps, and path planning. See [Murphy, 2000] for an excellent discussion of occupancy grids. See [Thrun, 1998] for a principled and well-engineered integration of metric maps and topological maps; in particular, the information and figures on the following pages nicely complements our class discussions.

| [Dean, 1999] | Dean, T., Lecture notes on basic probability theory, 1999. |
| [Dean, 2002] | Dean, T., Lecture notes on updating occupancy grids, 2002. |
| [Murphy, 2000] | Murphy, R., An Introduction to AI Robotics (Intelligent Robotics and Autonomous Agents), MIT Press, 2000. |
| [Thrun, 1998] | Thrun, S., Learning metric-topological maps for indoor mobile robot navigation, Artificial Intelligence, 99(1) 1998. |