
Braitenberg commenting on the behavior of Vehicle 1: "Anyway, you would say, it is ALIVE, since you have never seen a particle of dead matter move around quite like that." Mention the response of the attendees of conferences such NCAI who have participated in various social events attended by robots, e.g., robots carrying groceries and serving hors d'oeuvres, or museum visitor confronted with robot guides. Simple behaviors combined to achieve complicated emergent behavior.
Physics matters, but for simple service robots dealing with environments such as offices, factories and homes, common-sense physics is often quite adequate; of the various physical mindsets including that of Aristotle, Galileo, Newton, and Einstein, my guess is you can get a lot of mileage out of the first, the velocity of an object is proportional to the force acting on it, rarely need the second and third, force is proportional to the mass times the acceleration, and never need the last. In any case, knowing the physics needn't require knowing the equations of motion or being able to solve differential equations. Getting the physics "right" means not only getting it right qualitatively, i.e., knowing what quantities are dependent on what other quantities, but getting it right quantitatively, i.e., knowing the constants of proportionality or at least behaving as if you know the constants to some precision. It took Galileo and Tycho Brahe to make the painstaking observations that overturned to Aristotelian view and even faced with experimental data that appeared to undermine the Aristotelian view they found it hard to accept alternative interpretations.
Braitenberg's comments about knowledge in Chapter 3 are right on the mark. Programmers imbue robots with knowledge often in a procedural (rather than declarative) form which can make the knowledge opaque and difficult to extract or extend. This knowledge captures important, practical characteristics of the physics of the robot's world. What if the physics changes, slippery surfaces like ice skating rinks challenge Aristotelians? To what extent do you think that terrestrial animals, say a toad or a bird, could adapt if there was a major change in the physics governing the world? For example, what if the gravitational constant changed significantly so toads could hop for miles instead of meters, or, more radically, what if there was no gravity at all?
So far we've concerned ourselves with combinations of simple behaviors. Before we move on to coordinating behavior, it should be noted that even simple behaviors relating the level of the output of a sensor to the level of the input to an effector are typically quite complicated whether in the case of robot or in the case of an animal. For example, the voltage or output of an analog-to-digital converter hardly ever has a linear relationship to the quantity we think we're measuring, e.g., "light level" or "temperature". In addition, we can seldom directly govern the quantity that we want to control; for example, we'd might want to control the velocity of a robot but all we can try to do is control voltage level for a motor and that may depend on our batteries or additional circuitry. The actual velocity will depend on a multitude of frictional forces, the operation of internal flywheels and the current speed of the motor, the load the robot is carrying and the incline the robot is trying to negotiate, many of which can't be even sensed much less controlled.
Braitenberg's example of a nonlinear response in Figure 6 of Chapter 4 is one of the simplest such behaviors. Typically, we'll be dealing with component behaviors, i.e., "simple" behaviors, that are governed by computer programs that invoke nontrivial calculations relying on logic, geometry and the calculus, and keep internal state; in contrast with the programs for, say, handling database queries, these programs are relatively simple; however, their behavior when interacting with a complex environment such as the one we live in day to day, can be very complicated - dauntingly so. Braitenberg mentions that it is impossible to infer structure/mechanism from behavior simply because there are multiple machines that realize the same behavior - this complicates the job of the neuroscientist trying to understand the brain. However, even if you know the mechanism, i.e., have a program or wiring diagram, it is still quite hard to explain exactly how the mechanism results in the observed behavior - this complicates the job of the engineer trying to debug the mechanism or explain its function.
Chapter 5 is about using logic to orchestrate behaviors. Braitenberg makes the point that while internal memory is useful, it is not absolutely essential given that you can "leave marks in the sand" in order to store state information externally. I expect you can easily imagine cases in which it quite convenient to have internal state, e.g., keeping track of which plants are poisonous and which are nutritious, and other cases in which it is valuable to store information externally, e.g., carving notches in trees to mark the path you're following so you can reverse your steps if need be. What do these different examples say about our ability to sense and make distinctions?
I recommend that you read all of Braitenberg's book. It's fun, it's thought provoking and it may give you some ideas on how to build simple robots. I can't comment on the correctness of the biology and neurophysiology; the book was first published in 1984 and many things have happened in biology and neuroscience since that time. It was not for it's biological insights that I chose this book for CS148, but rather for its insights regarding how simple behaviors can give rise to more complicated, often seemingly intelligent, behaviors in the presence of a complicated environment. We'll return to this them later when we consider the behavior of collections of robots.
Neuroanatomists and cybernetician such as Grey Walter and Valentino Braitenberg were interested in neural pathways, feedback circuitry, and, ultimately, complex emergent behavior. Emergent behavior is behavior that arises out of the interaction of simple component behavior; often specifically behavior that is unpredictable in the sense that the easiest way to predict it is to actually cause it, say, by running a program that embodies the simple behaviors and their interactions.
When an engineer talks about positive feedback he or she is generally talking about an unstable system; you may want positive feedback in your day-to-day lives, but an engineer wants none of it. Negative feedback refers to reducing errors to bring a system closer to a target of "goal" state in which the error is zero.
The input signal to a feedback controller is often called the "desired" or "goal" state. However, saying that your furnace has the goal of keeping your house at the desired temperature does seem a little presumptuous. Anthropomorphizing inanimate objects (i.e., attributing human form or personality to things not human) is generally frowned on in engineering, but it's done all the time in robotics and we'll do it often but guardedly in this course.
Perhaps it would be better to say "the furnace acts in a way to make the error signal equal to zero" but in terms of communication, the language of goals, desires and intentions is often very useful.
Braitenberg's vehicles are gedanken (or thought) experiments designed to get you to think about simple systems that interact with their environment. Just as Einstein's gedanken experiments have helped many physicists and laypersons alike gain some appreciation of general relativity, so these experiments should provide you with insights and meditations that are good to come back to frequently.
A word about studying grey matter. It is only in the last decade or so that we've gained any real insight into the anatomy and physiology of the brain. If you take a course in neuroscience, you'll learn about such brain structures as Golgi cells. (Golgi cells are cells in the cerebellar cortex; they are believed to play an important role in governing motor activity. Golgi cells are named for Camillo Golgi who is probably best know for his preparations and methods of staining brain tissue so as to better identify particular structures. We're just beginning to map out the structure in higher organizations.) Walter and Braitenberg were fascinated not only with the brain and how it got things done, but with what it got done, behavior, and how such behavior might come about quite apart from brains or biology. Neural pathways suggested circuits and circuits suggest computation.
To see the flow of ideas from "meat" to machines (Braitenberg's vehicles), start by thinking about a blob of flesh that's capable of locomotion - the cilia or flagella of a paramecium or the protoplasmic flexing of an amoeba. Now make it responsive to outside stimuli. Let the responsive part separate from the motor part say on a stalk or other extension. Now imagine these stalks waving about or arranging themselves in patterns or circuitry. Now think "Vehicle 1".
Just a couple of points to add to the discussion of Braitenberg's Vehicles. Braitenberg's lovely abstractions aside what would you expect from the following:

Perhaps the most obvious thing to notice about the above is that there are no units specified and no reason to believe that motor units stand in any reasonable relationship to light units. It could be, for example, that the maximum value for the light sensor is below the minimum value required to get the motors to even turn. One way to produce a more reasonable mapping of light units to motor units is to normalize one to the other. In the following, we convert light sensor readings to 0-to-100 motor power levels.

There are a number of things to notice about this procedure. (Besides the fact that I put the declarations for the maximum and minimum light constants inside the procedure definition!) The first two declarations determine the min and max light levels. Notice that the minimum is more than the maximum; this reflects a property of some light sensors (and in particular the ones we're hypothesizing here) that smaller values indicate larger light levels. The declaration for the output variable accounts for the zero offset (subtracts MAX_LIGHT), scales the result (multiplying by 100/(MIN_LIGHT - MAX_LIGHT)), and then subtracts the result from 100 (a larger light reading should result in a smaller motor command). The two conditional statements provide sanity checks on the resulting output value. Now our vehicle control program looks like:

The linear function implicit in normalize may be inappropriate in some cases, e.g., the light sensor may respond logarithmically with respect to the level of light measured in terms of, say, Lumens (a photometric (visual) unit of measure comparable to the radiometric (physical) unit of the Watt).
Another concern raised by the normalize function is that we may not know the minimum or maximum light levels that we'll encounter in practice. The solution to this problem is to gather data at run time and compute the minimum and maximum values on line. (And this time I've put the constant declarations inside of the while loop!)

There are also occasions in which we want there to be a minimum level that evokes a response. In this case, we might set a threshold value, say the average light level, to use in determining whether to respond or not to a measured light level.

Thresholding constitutes a form of logic or decision making circuitry. It's interesting to consider how we might compute the average. In the following the (i,j) subscript correponds to the jth reading of the ith light sensor. The following expansion of the average function suggests how to calculate a running average:
![]()
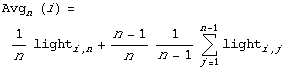

Except for the need to keep track of n this seems perfectly reasonable and easily implementable. What is the advantage of keeping a separate average (and thus threshold) for each of the light sensors?
One possible problem with the above averaging and thresholding method is that the light levels may change. Such a change could be due to the light source itself brightening or dimming over time, or to the robot moving into a region with different light sources, or to the robot's sensors physically degrading or being partially obscured by dirt or even parts of the robot such as a manipulator. Consider the following alternative to computing a running average:
![]()
This looks a lot like our running average except that the continuously changing 1/n is replaced with the Greek letter Beta (clearly an improvement on this score alone) representing a constant between zero and one. How does this really change the behavior of the robot and is this a desirable change in all cases? What potentially desirable characteristic of biological memory does this implement in a robot?
We can add sensors to our robot and combine the various behaviors in Braitenberg's robots with new behaviors. As in the case of the behaviors manifest by Braitenberg's vehicles, the behavior resulting from simple programs may not immediately be obvious but only emerge as a consequence of interaction with objects in the robot's environment. Consider the following robot program and hypothesize the behavior you might expect if the robot finds itself in the corner of a room.

How might we avoid this seemingly "pathological" behavior? One approach might involve adding a little randomness to the robot's behavior. How might this help? Another approach is to have some "monitoring" procedure that could recognize pathalogical looping behavior and break the robot out of the loop. Note that the monitoring procedure could be as simple as a "time out" which terminates a control loop that takes longer than expected; in an animal, we might interpret the abrupt termination of a loop manifesting a very determined behavior as "boredom" or "frustration".