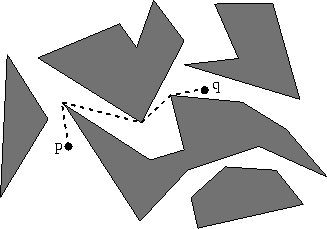
Figure 1: A shortest obstacle-avoiding path connecting points p and q.
ACM Computing Surveys 28A(4), December 1996, http://www.acm.org/surveys/1996/ChenDeveloping/. Copyright © 1996 by the Association for Computing Machinery, Inc. See the permissions statement below.
Abstract: Computing shortest paths is a fundamental topic in computational geometry and arises in many applications. We assess the status of the current research on solving geometric shortest path problems and suggest several possible directions for future work on these and related problems.Categories and Subject Descriptors: F.2.2 [Analysis of Algorithms and Problem Complexity]: Nonnumerical Algorithms and Problems - Geometrical problems and computations
General Terms: Algorithms, Design, Theory
Additional Key Words and Phrases: Computational geometry, shortest paths, optimization, implementation
The problem of path planning is in general concerned with finding paths connecting different locations in an environment (e.g., a network, a graph, or a geometric space). Depending on the specific applications, the desired paths often need to satisfy certain constraints (e.g., obstacle-avoiding) and optimize certain combinations of criteria (e.g., various distance metrics and cost functions). A well-known example of path planning problem is that of computing shortest paths in graphs [Fredman 1987] (i.e., finding a path in a graph connecting two vertices with the minimum total length). The problems of planning shortest paths arise in many disciplines, and in fact are one of the several most powerful tools for modeling combinatorial optimization problems.
The geometric version of the shortest path problem can be stated as follows: Given a d-dimensional space scattered with obstacles, compute a path P connecting two points p and q such that the path P does not intersect the interior of any obstacle and that the total length of P (based on a certain metric such as the Euclidean) is minimized. Figure 1 gives an example of such a path in the plane. There are many variations of this problem.

Figure 1: A shortest obstacle-avoiding path connecting points p and q.
Computing shortest paths is one of the most fundamental topics in computational geometry. Geometric shortest path problems play an important role in many practical applications (e.g., geographical information systems, operations research, plant and facility layout, robotics, transportation, and VLSI design). Also, they have significant connections with other fundamental topics in computational geometry (e.g., convexity, visibility, Voronoi diagrams, triangulation, and geometric optimization) and with other disciplines (e.g., graph theory, combinatorial optimization, and networks). For example, geometric path planning problems address quite naturally the combinatorial and algorithmic aspects of robot motion and navigation.
In the past two decades, a great deal of research work has been done on solving geometric shortest path problems, especially for the planar and 3-dimensional (3-D) settings (see [Mitchell 1996] for a survey). For computing shortest paths in the plane with polygonal obstacles, Hershberger and Suri [Hershberger 1993] developed an optimal O(n log n) time algorithm (where n is the total number of obstacle vertices). For computing shortest paths in the 3-D space with polyhedral obstacles, Canny and Reif [Canny 1987] showed that the problem is NP-hard, and several efficient approximation algorithms have been discovered (e.g., [Choi 1994]). However, despite of the significant progress already made, much research work on geometric shortest paths and related problems remains to be done. Besides the importance and applicability of these problems, the following reasons also motivate further research in this area.
In view of the above reasons, we believe the following are important directions for geometric shortest path research in the coming future.
We think it is necessary to develop simple-to-implement yet reasonably efficient algorithms for more general geometric path planning systems. For many applications, the geometric environments can be very complicated, and thus algorithms hinged on specific geometric structures may be of little use. Therefore, it is highly desirable to design shortest path algorithms that work in some ``general'' geometric settings in an efficient manner. The notion of algorithmic efficiency for such solutions might depend less on the ``standard'' input size of a problem but more on the ``configuration'' of the input (e.g., an octree-like partition of a 3-D obstacle-scattered environment). The paths obtained by such approaches may not be truly shortest but may be very good approximations. The framed-quadtree and framed-octree approaches [Chen 1995b] are a few such examples that are relatively effective yet simple to implement, and could even be extended to higher dimensional spaces than 3-D.
We also believe that serious efforts must be made by the computational geometry community to reach out to applied fields, and that implementing geometric algorithms is an important step in this direction. It is very encouraging that quite a few projects on implementing geometric algorithms are currently under way. However, more efforts should also be made at a higher level of geometric software development. For example, it would be very useful if some tools are available for the automated design of computer programs for geometric shortest path problems. A user could use a ``geometric problem specification language'' to describe a problem that he/she wants to solve. Then a tool set would process this problem specification program from the user and generate target programs in a desired programming language for the needed geometric computation (like Lex and Yacc for constructing components of compilers). Such tools would greatly enhance the accessibility of geometric algorithms to many users. A base to the development of such high level design tools for geometric computing is to make geometric algorithms available not only on paper but also as software.
It is anticipated that further research on developing new algorithms and software for geometric path planning problems will have a great impact on the theoretical study and practical applications of computational geometry. In particular, such work can become relevant to the following application areas: Military applications (e.g., route planning for special operations aircrafts and vehicles), NASA's Remote Exploration and Experimentation program (e.g., autonomous spacecraft path and exploration planning), Geographical Information Systems (e.g., route planning on electronic maps), and robotics (e.g., robot motion and navigation). It is even likely for the work to touch an average person's daily life in the future (e.g., a route planner on cars for tourists or for avoiding traffic jams in daily local traveling).
Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from Publications Dept, ACM Inc., fax +1 (212) 869-0481, or permissions@acm.org.