RIGID BODY DYNAMICS

• What are Rigid Body Dynamics - A subset of computer simulation that deals with how to represent and implement the animation or dynamic simulation of a rigid collection of points.

• Basic Physics - How to find momentum, etc.

• Representing State at Time t - What information is needed for different types of representations.
  
  • Particles vs. Rigid Bodies

• Collision Response - When we know a collision has occured how do we change the state of the 2 objects that collided.

Simulating the motion of a rigid body is based on simulating the motion of a particle.

Let a function x(t) denote the particle's location in the world space at time t.

The function : 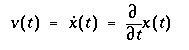gives the velocity of the particle at time t.

The state of a particle at time t is the particle's postion and velocity.

This concept is generalized by defining a state vector Y(t)for a system: for a single particle it is:

When actually implementing the Y(t), Y(t) can be described as an array of 6 numbers. Typically the first 3 elements of the array represent x(t), and the last 3 element of the array represent v(t).

In order to actually simulate the motion of a particle we need to know the force acting on the particle at time t. The function F(t) is the sum of all the forces acting on the particle: e.g. gravity, wind, spring forces, etc.

If you're dealing with rigid bodies and not just particles, to determine the position of the object you also need to find its orientation in world space which is given by:

f=ma

P(t)=M*V(t)         Momentum = Mass * Velocity


A(t) = F(t)/M

Where:
P(t) is Momentum at time t.
A(t) is accelerationt at time t.
And F(t) is the force.

Distance between 2 points in 3-space:
d = sqrt( (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 )

In order to simulate the dynamics of a rigid body at discrete time steps we must use some form of integratiom. In order to calculate the position at each time step in the x,y, and z (3-space), we need to store information for each body acting in the system.

Basic Formulas To Update Position at each deltaT
S(t) = I + (V * t) + (.5 * A * t^2)       [1]
this is just the integral of
V(t) = Vi + A*t				 [2]

Where:
I = Initial Position  (Old Position).
S(t) = New Position (after time step).
V = Velocity
t = Time step
A = Acceleration, calculated  A = f/m

The data structures representing our particles must store the following state information in order to simulate particle dynamics.

• Mass
• Velocity
• Position - center of mass.
• Force Acting on the Body

Rigid bodies include rotational information, and information representing the change in orientation over time (delta R(t)). Rotations are stored as quaternions to allow for easy addition and multiplication of rotations, to avoid numerical drift, and to minimize state information.

Representing the change of orientation with time can be done in a variety of ways that is usually game specific. For example:

Above we see the equation for calculating torque which can be useful for certain types of collision response.

• An angular velocity value can be stored in addition to the orientation quaternion. This can simplify the task of finding the torque which can be useful when using angular momentum to calculate the affect of a collision on the orientation change over time.
• In other cases we may want to store another quaternion which is composed with the orientation at each unit time.
• Of course never do more than you have to in your game. If you're in 2D you can just store a scaler representing how much your rotation changes with time.

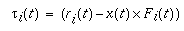
Example - Space Kombat - Asteroids which rotate and collide realistically (breaking up relative to energy of collision), and rotating differently based on the angular momentum of the object that was collided with.

With the state information above we can use the Force to find the Accleration along each axis, which we use to update the position (formula #1). From the Mass & Velocity we can then calculate Momentum which is conserved in any collision (simulation dependent), and thus can be used to get proper collision response.

Example - 2-D bumper car simulation, in which you have n-body collision detection and response. All bodies have a force constantly acting on them. Room keeps track of finite number for force sources, each body computes sum of forces acting on it based on its position.

Getting nice approximations of collision response when doing discrete simulations is tricky because its impossible to know exactly when a collision occured. Any simulation is game specific but most formulas for doing collision response are based on the idea of conservation of energy.

First issue is collision detection when doing discrete computation. An enlarged bounding box based on current and last position can be helpful to detect cases where objects collide in the middle of a time step. However once an extended-bounding box intersection is detected a binary search may be necessary to find if and when a collision actually occured between the bodies.

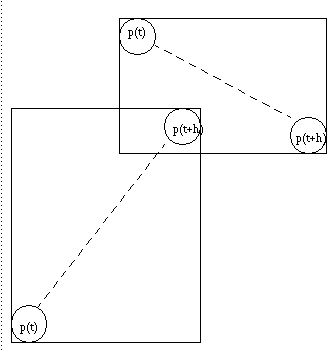
If we know approximately when in a time step a collision occured. At that time of collision we can compute the new velocity as a result of the collision, and then use that to find the proper position based on the fact that the particle changed direction midway through the time step.

Expansion of inner product

2-D Reflected Vector:

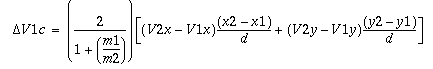
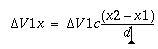
When say 2 spheres collide each has a component of their vector which is projected along the vector d which is the position of sphere 2 minus position of sphere 1. In other words each sphere exerts a force on the other from its center to its point of collision with size relative to its momentum. We then need to compute the change in that force (reflected force), which can then be used to update the velocity vector by adding to it a reflected vector.

In some cases it may make sense to find the exact time of collision analytically, in others the collision can be thought of as sticking until time step through, at which point they bounce off each other (what if they collide with low momemntum?). Or in some cases if the 2 spheres overlap at the end of the time step, they can merely be repositioned so they are touching and then reflected, but in some cases this can be inaccurate.

Example - 3-D game of pool. Collisions must be represented accurately even if they occur between a time step.