CS 195-G: Face Morphing
The goal of this project was to implement face morphing and morph between the different faces of people in the class.
Algorithm
The face morphing algorithm morphs between faces using a common set of feature points, placed by hand on each face. To morph between two faces, you need to warp both faces to a common shape so they can be blended together. It can be viewed as a hole filling problem where the constrained pixels are the known warp offsets at each feature point, and the unconstrained pixels are the unknown warp offsets elsewhere. We can then use poisson blending to complete the warp, resulting in a seamless warp image that defines the offsets to the original image at each point. To warp each face, we just sample the original image at the warp offset.
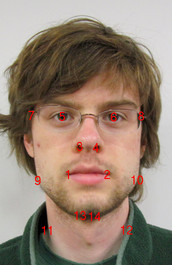 Starting image with points |
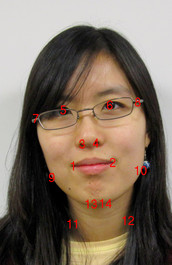 Ending image with points |
The images below are of a 50% warp (an average) between the two faces. The grayscale images represent the x and y offsets, where gray is a zero offset, white is a positive offset, and black is a negative offset.
 X offset of warp |
 Y offset of warp |
 Warped image |
 X offset of warp |
 Y offset of warp |
 Warped image |
I was not satisfied with the results of my poisson interpolation. The interpolation points can clearly be seen in the grayscale warp images, which means they had very a local effect (the warp is seamless but not smooth). This can be seen especially well on the neck of the first face. The problem could be fixed by adding more points between the original points, but you shouldn't have to do that. I'm not sure if this is a problem with my code or because I constrained the edges of the warp image to zero, but something didn't work right. I ended up implementing the Beier-Neely algorithm, which worked out much better.
Beier-Neely Algorithm
I also implemented the Beier-Neely image morphing algorithm. Beier-Neely morphing interpolates lines, not points, and defines the warp as a weighted average of the warp for each line. It was the algorithm behind Michael Jackson's Black or White face morphing sequence.
To create the warp for each line, the pixel to be warped (X in the images below) is first represented in a basis with axes parallel and perpendicular to the line PQ. The temporary coordinate is (u, v), where u represents the percent along the line and v represents the distance from the line. To get the new coordinate, we get point X' using (u, v) and the basis for the new line P'Q'.
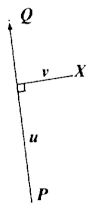 The original basis |
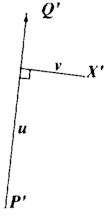 The warped basis |
 |
This generates one warp per line, each of which is a simple rotation and non-uniform scale (scaling is only done along the axis of the line). These warps must then be averaged to get the final warp. In the original paper, the weights for the average are tuned with the formula below. The dist variable is the distance of the point from the line segment, and the length variable is the length of the line segment.
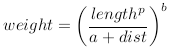
The equations give several parameters to tune, and I got the best results when a = 0.001, b = 2, and p = 0. Ignoring the length of the line segments (by setting p to zero) gave better results than when the length was taken in to account. I used seven contours with 28 line segments to represent the features of each face.
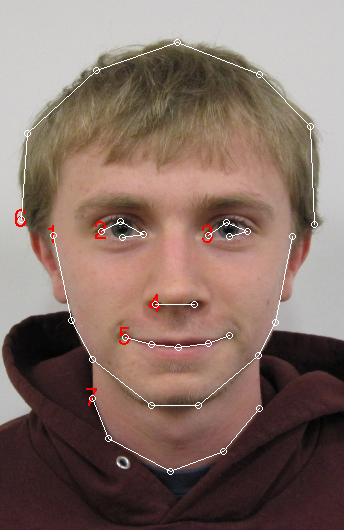
The seven contours used
Even though the complexity of the algorithm depends on the number of lines, my implementation was able to render three frames per second with no artifacts.
Results
Face morph of the class

Average face
I also tried morphing white cars. The results work less well then people because they have sharper features, but the Beier-Neely algorithm really helped because it allows you to specify that certain lines stay straight, which you can't do when just specifying points.
Car morph

Average car

The twelve contours used