CSCI1290 Final Project: Coded Aperture
Sorawis Sangtawesin (ssangtaw)
May 10, 2011
Project Description
The main goal for this project is to experiment with the coded aperture as described in the SIGGRAPH 2007 paper by Levin et al. By following the instructions given in the paper, I expect to be able to do depth-estimation on the image with the calibrated blurred kernel and apply a deconvolution to get an all-focused image.The coded aperture will be of the pattern similar to the one given in the siggraph paper. I will also try other patterns which does not require a significant drop in the exposure so that this method may be more useful in practice. The aperture will be cut and put on the front of the Canon 85mm f/1.8 lense instead of taking apart the lense. In fact, I have tried this method before and it worked well in producing the aperture-shaped blur, although at the time my aperture does not have a coded pattern. Here are the sample:

The aperture patterns that I experimented on are:
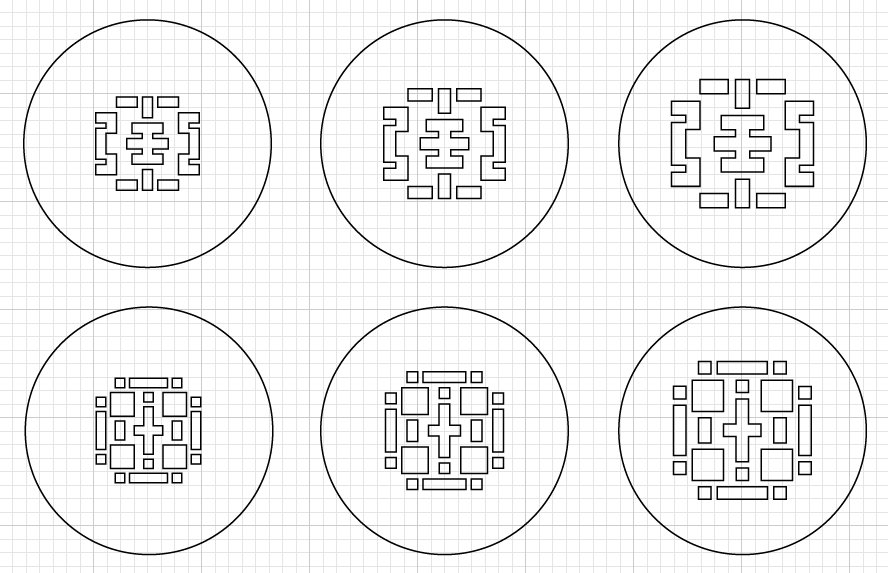
There will be three sizes for each filter because I do not know what the maximum possible value is. The theoretical value is 85mm/1.8 = 47.22mm at the aperture location, so I am making the filter being as large as 40mm.
After getting depth estimates by applying different deconvolutions in a small window, I will try to reproduce all-focused images and refocused images. If the automatic depth estimation fails, I will manually specify depths of the objects and try to reproduce the images instead. Regardless of the depth estimation algorithm, this method will allow for us to take pictures without having to focus and then use auto/manual depth estimation to get a desired focus computationally.
Algorithm
The algorithm I wrote splits up the images into small patches, tries to apply several deconvolutions to them and measure how well the deconvolutions are. This measure is done by reapplying the convolution to the result and compute the SSD between the resulting image and the original image. (High-pass filter is applied to both images once to get rid of the low-frequency signal. The reasoning is similar to project 1) The choice of deconvolution I have chosen is the L2 deconvolution in the frequency domain since it produces the most detailed result. And because this type of deconvolution also produces the ringing effects, it will be more prone to errors when a wrong kernel size is used for deconvolution, making the best scale more distintive. Moreover, it runs a lot faster than the sparse-prior deconvolution (~5 sec vs ~1000 sec for a 5MP image)After this computation, all the patches where the minimum-sized kernel produces the best result are assumed to be associated to the area which are in focus. This is because if they were already in focus, applying any deconvolution will always results in a blurry image. (It is useless to apply extremely small deconvolution to the image and compute SSD, because in the limit where the kernel becomes an identity, the SSD is obviously zero.) Hence, I reset all the patches with the minimum depth to zero (in focus) and do nothing in the final deconvolution.
After the depth estimation is done, I apply the sparse-prior deconvolution to the image with varying kernel sizes according to the data from the depth estimation. The runtime is approximately 20 minutes for a 5MP image.
Setup
The aperture is attached to the front thread of the lense as shown below. The camera used is a Canon 7D. Photos are taken at the full 18MP resolution and then the center part was cropped in order to minimize the distortion from the lense.
I also found that it is more accurate to use the focus distance from the EXIF information produced by the camera to get the exact distance to the object in focus. Then measure the distances to other objects relative to the focused object.
Calibration
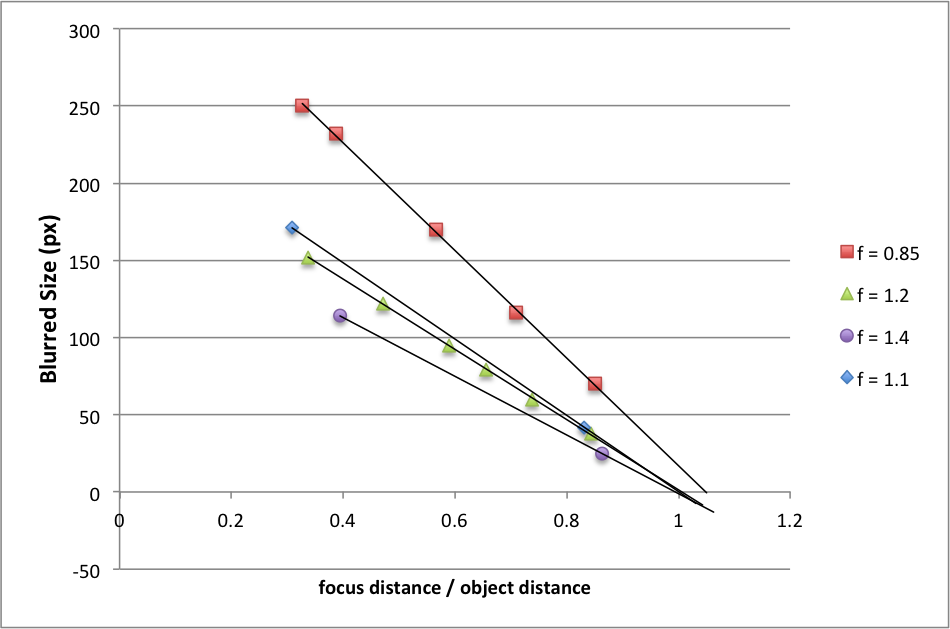
Several calibration photos of an LED light were taken at different focus distances. By looking at the data and considering the form of the thin lens equation,
Result

From left to right: (1) Original Image, (2) Richardson-Lucy Deconvolution, (3) L2 Deconvolution w/ smoothness=0.01, (4) L2 Deconvolution in freq domain w/ smoothness=0.01, (5) Sparse prior deconvolition w/ smoothness=0.01, (6) sparse prior deconvolution w/ smoothness=0.05
Sample Case
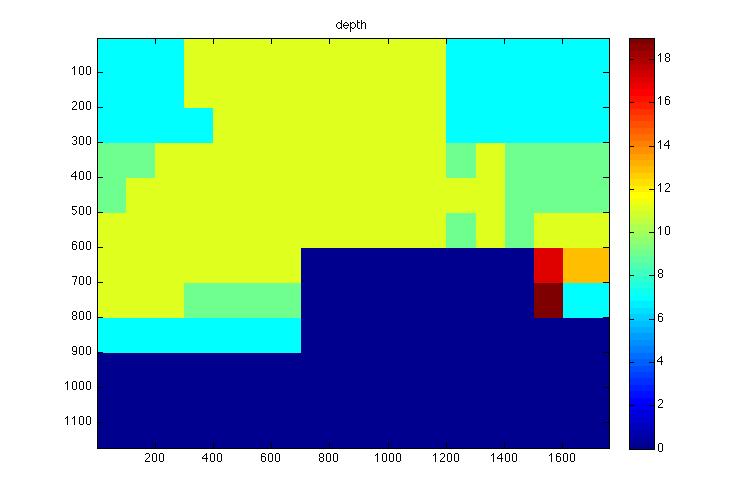
Note that because of the lack of distance information, the depth information in this case is displayed in terms of the blurred kernel size. |
|
 |
|
 |
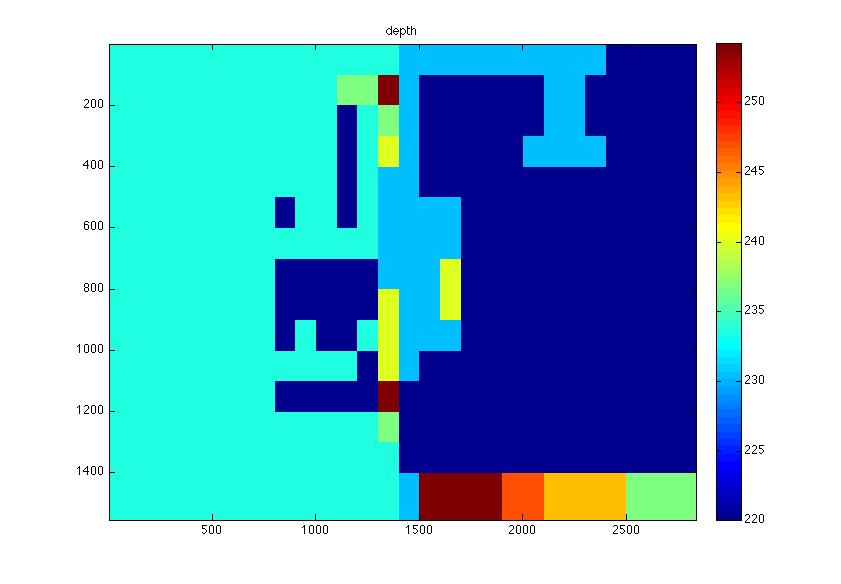
My Own Test Case
 |
|
 |
|
 |