CSCI1290 Computational Photography - Final Project
Colorization Using Optimization
Kefei Lei (kefei)
May 15, 2011
 |  |  |
Overview: Goals and Approach
Colorization of grayscale images is a very practical problem. Using available image processing and manipulation tools, an artist needs to spend tons of time to make the colorization convincing. Anat Levin et al. prensented a simple algorithm [Levin 2004] to generate a colorized image based on just a few casually scatched scribbles by a human user. It is based on an insightful oberservation: nearby pixels with similar intensity values should also have similar hues. This gives rise to a quadratic error function for each pixel and the scribbles puts a set of linear constraints on the system of equations formed by all the pixels in the image. They are then solved to find color values for all the pixels.
The Algorithm
The algorithm works in the YUV color space, where Y denotes the intensity, and U, V are the coordinates on the color palette. The input to the algorithm is a set of pixels with only intensity values (Y), while some of them are constrained by full YUV values. The output is the YUV value for every pixel. For each pixel, define its relative weighted color difference to all its neighbors, in terms of both U and V values (here only the V version is shown. Solution for U is by analogy).
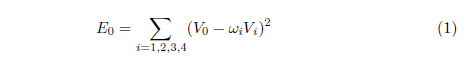
where the subscripts 0 refers to the pixel of interest, and 1, 2, 3, 4 refers to the pixels to the top, left, bottom and right to pixel 0, if any at all. The w's are weights that sum to 1, and are larger if the two pixels have similar intensities (Y), small otherwise. In the implementation, I use a Gaussian-like function:
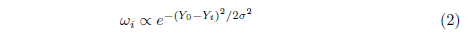
Where the variance is calculated within a 5x5 window around pixel 0. Expanding equation (1), we have
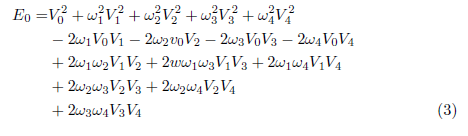
Because it is a quadratic function of the V values, it can be written in matrix form:
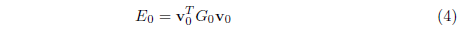
where the vector v_0 are the V values of the five pixels in the order 0, 1, 2, 3, 4. and the matrix G_0 is given by:

This error function is minimized when pixels with similar Y values have similar V values as well. The sum of errors of all pixels can be obtained by expanding the vector v_0 and matrix G_0 to include all pixels in the image, putting each entry of G_0 in the corresponding position in the larger resulted matrix, and then adding all of them up. The result can be written as:

where v is the vector of all the V values, of length mxn, and G is an mn x mn sparse matrix (assuming the input image is mxn). Our goal is to find the v that minimizes E. Since some of the values in v are set by the user (using the scribbles), we rearrange v and G, and write E as:
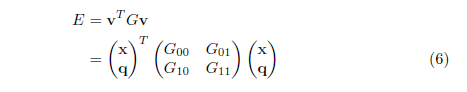
where x are the V values for unknown pixels and q are V values for constrained pixels. The matrix G is rearranged and divided into four parts: G_00 contains the columns and rows corresponding to unconstrained pixel,s G_01 contains rows for constrained pixels and columns for unconstrained pixels, and so forth. Taking the derivative of E and setting it to zero, we have:
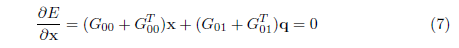
or written as
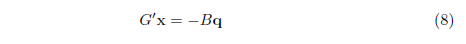
and x can be solved using LU factorization of G'.
Implementation and Known Bugs
The MATLAB code for the paper is available online, so I implemented the algorithm in C++, using Qt as GUI framework. The interface is rather intuitive and self-explanatory. The user can choose color from a HSV color picker, and controls the brush width. Undo and redo operations are supported to allow progressive colorization and trial and error, which turns out to be very important for producing good results. The implementation is rather unoptimized: it now does linear search on constrained pixels when rearranging the matrix G. As the number of scribbles increase, it becomes a bottle neck for the running time of the program. An improvement would be to pre-compute an image that encodes information for each pixel and just do an image lookup. The program also have occasional memory leak programs with progressive colorization.
Results and Discussion
Requirement on Input
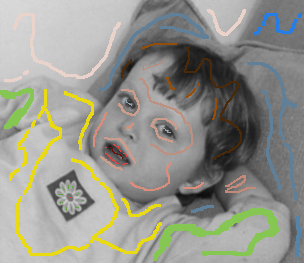
Even though the input can be casual and imprecise, the choice of color greatly affects the output. It is natural for a human being to choose color in their mind from a color palette, but the color picked up has all of the YUV component, whereas the constraint only needs UV. The UV values, combined with the input Y, does not necessarily give the color that the human originally thought of. Therefore picking colors correctly is a non-trivial task. The following picture shows the difference. In the second row, the colors were more carefully chosen and adjusted through trial and error, and the result looks much more realistic than the first row.
| Grayscae | Scribbles | Result |
 |
 |
 |
 |
 |
 |
The weight function plays a vital role in the behavior of the colorization. A flat weight function (one that does not vary much according to intensity difference) tends to "smear out" the colors and blend them better, but does not respect boundaries much. A peaked weight function gives great color cutoff at intensity boundaries, but often fails to interpolate any color at very dark regions. In practice, a flatter function is preferred and we compensate that by putting scribbles closer to intensity boundaries. In the pictures above, not that the color in the kid's left sleeve bleeds out to the pillow, and it is fixed in the second row by adding a scribble at the boundary.
Progressive Colorization
It is very hard to get the input right at the first time. It is necessary to incrementally colorize the image by adding new scribbles and deleting undesired or ill-colored ones. The following images illustrate the process.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
More Results
And finally, an attemp to colorize a black-and-white photo taken around 1980 in northern China. That's my mom when she was younger than I am now. |
 |
 |