 |
 |
 |
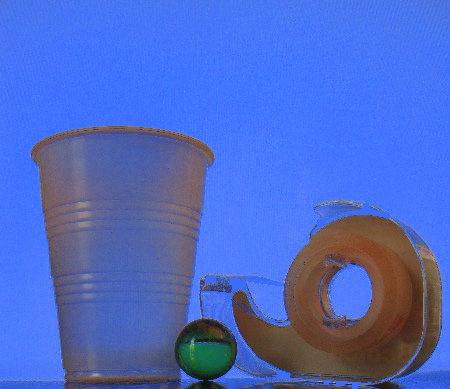 |
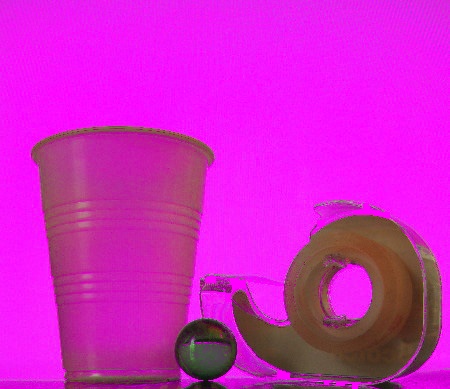 |
Image Matting
Alicia Boucher -- aabouche
PDF of paper implementedThe reference Images were photographed in front of monitor with as little camera movement among sets of reference images as possible. I searched online to find the background image scenes. The images were loaded into MATLAB to be composited.
Note: the images with the black borders are reference images that were photographed or scene backgrounds. The images with thick bright borders are the combination of a new scene background with the foreground from the reference image.
Blue screen matting
Blue screen matting requires a reference image of a non-blue foreground against a pureblue background. The blue background from the monitor did not photograph as pure blue and light reflections onto the foreground caused confusion in the algorithm. For pixels what were significantly more blue than they were either red or yellow, an alpha value was calculated to be one minus the pixel's blue channel. This solution did not wor well for the image below. All three of the results are entirely tinted blue because the reference background was not pure blue. For this same reason, the water bottle blends into the rest of the constructed scenes.
 |
 |
 |
 |
Blue screen matting with known background?
Even when attempting to remove the background when the background is photographed separately is difficult because corresponding pixels do not match exactly.
 |
 |
 |
Triangulation
Another solution to constructing a new foreground-background combination is triangulation matting. Triangulation requires the foreground photographed against two arbitrary backgrounds and photographs of those two backgrounds. In my examples I chose to use single colors in each of the backgrounds. The steadiness of the camera was not guaranteed, so if it moved slightly then there would be less of a problem with solid backgrounds because random backgrounds are more difficult line up. However, the backgrounds are not purely solid colored, and, as in the blue screen matting example, the target color was photographed as a different color. There are unintentional gradients on some of the backgrounds, but this is fine because triangulation should work on any two backgrounds. however, the two backgrounds must be different everywhere.
On the example below, the backgrounds do not differ on the glare of the light and the accidentally photographed scroll-bar on my monitor. Thus, these two elements appear in the new image when it is composited with the rainforest scene on the bottom left.
denominator=(Rbg1-Rbg2)^2+(Gbg1-Gbg2)^2+(Bbg1-Bbg2)^2
alpha=numerator/denominator
For each pixel of conceptual image, the foreground, an alpha value is calculated based on the equation in the Blinn paper in Theorem 4. Next a matrix A is created with is diagonal entries set to the alpha values. Three solutions, b, are constructed for each channel. Each entry of the solution is the difference of the the photographed forground color minus the contribution of the background color ((1-alpha)*color of the background image at that point). The r,b, and g channels for the foreground pixel colors are solved as closely as possible using matlab's right divide.
for k=1:numberOfNonzeroElements
index=indicesOfNonzeroElements(k);
[i,j]=ind2sub([w,h],index);
Ib(k)=index;
Jb(k)=1;
r_Vb(k)=r_fg(i,j)-((1-alpha(i,j))*(r_bg(i,j)));
g_Vb(k)=g_fg(i,j)-((1-alpha(i,j))*(g_bg(i,j)));
b_Vb(k)=b_fg(i,j)-((1-alpha(i,j))*(b_bg(i,j)));
end
^Constructing the solutions to the sytem of equations. fg is the foreground image and bg is the background image. I found that making the solution equation getting the values of the foreground color from a single image worked better than trying to get it form both images. In the following equation, fg1,fg2, bg2, bg2 are the corresponding background foreground images.
b_Vb(k)=b_fg1(i,j)+b_fg2(i,j)-((1-alpha(i,j))*(b_bg(i,j)))-((1-alpha(i,j))*(b_bg2(i,j)));
 |
 |
 |
 |
 |
 |
Triangulation: distinct hues
Using two different colors, as opposed to two different shades, did not produce very good results. In most cases the triangulation algorithm errs on the side of calculating too high an alpha value. In this case the problem is significant.
 |
 |
 |
 |
 |
 |
 |
 |
 |
Triangulation: green and white
I found that the compositing looked best when the reference images used backgrounds of different shades. I did not test very different shades with different hues. Using dark green and bright green worked fairly well on the example above. In the following examples I use a white and a bright green background. The results, however, are still not realistic when the new background involves multiple colors behind translucent foreground objects. Rays of light are refracted, scattered, and reflected in many semi-transparent objects, but this algorithm only calculates an apha value based on how much the reference background shows through.
 |
 |
 |
 |
 |
 |
solid colors
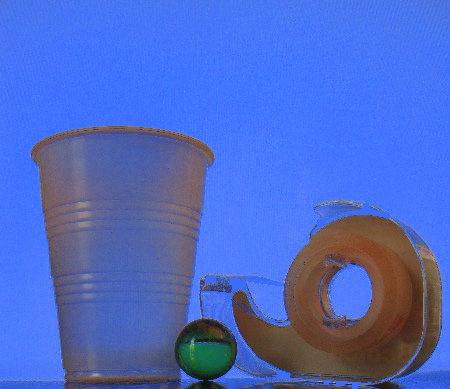 |
 |
More examples
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
solid colors

| 
|

| 
|