More on paths in graphs

We implemented this function for finding paths between airports. For each airport, it tracks the “previous” airport (the airport we got to it from) in the previous map. It then reconstructs a path from this map using the recursive reconstructPath function.

def reconstructPath(previous: Map[String, String], node: String): List[String] = {
  if (node == "") {
    return List()
  } else {
    return reconstructPath(previous, previous(node)) :+ node
  }
}

def path(graph: FlightGraph, start: String, end: String): List[String] = {
  var previous = Map(start -> "")
  var visit = List(start)
  while (visit.nonEmpty) {
    val node = visit.head
    visit = visit.tail
    for (neighbor <- graph.neighbors(node)) {
      if (!previous.contains(neighbor)) {
        previous = previous + (neighbor -> node)
        if (neighbor == end) {
          return reconstructPath(previous, neighbor)
        }
        visit = visit :+ neighbor
      }
    }
  }
  List()
}

The function above finds the path between the start and end airports (nodes) with the least number of flights (edges). We might want to find different paths. For instance, consider the graph below:

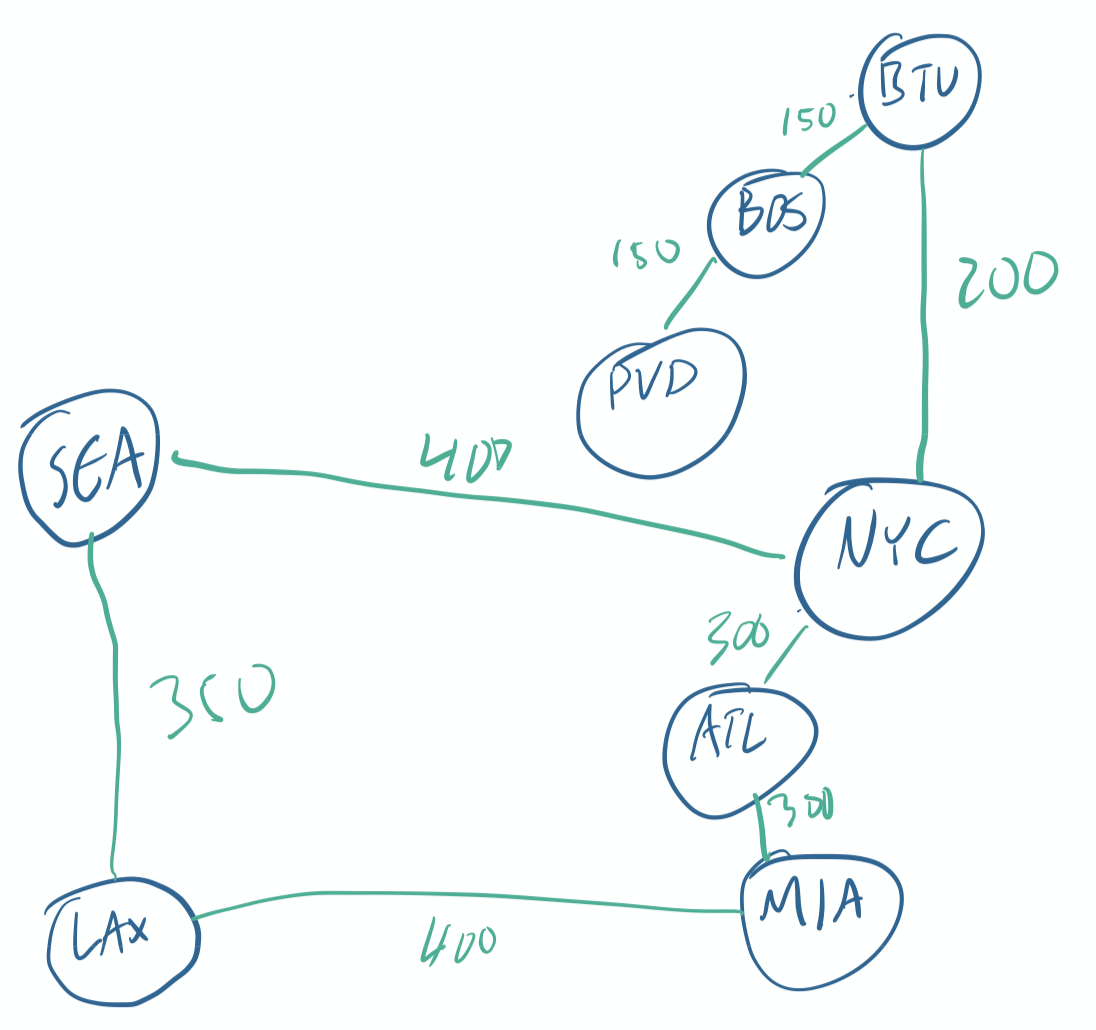
In this case, the shortest-length path between Burlington (BTV) and Los Angeles (LAX) is also the cheapest–BTV->NYC->SEA->LAX, with a cost of 200 + 400 + 350 = 950. But imagine that flights from New York to Seattle become much more expensive–say, $1000. Now our path from before has a cost of 200 + 1000 + 350 = 1550, and there’s a cheaper (but longer) path in the graph: BTV->NYC->ATL->MIA->LAX, with a cost of 200 + 300 + 300 + 400 = 1200. How can we find this cheapest path with an algorithm? We’ll talk about this next time.