Distances in graphs
Project 3
We discussed Project 3; see the lecture capture for details.
Flights
Let’s say we’re analyzing flights in the US, maybe to examine price differences between flying out of rural vs. urban airports. Our data are in CSV format:
BTV,NYC,200 BTV,BOS,150 PVD,BOS,150 MIA,LAX,400 NYC,ATL,300 ATL,MIA,300 SEA,LAX,350 NYC,SEA,400
How can we view these data as a graph? How about something like this:
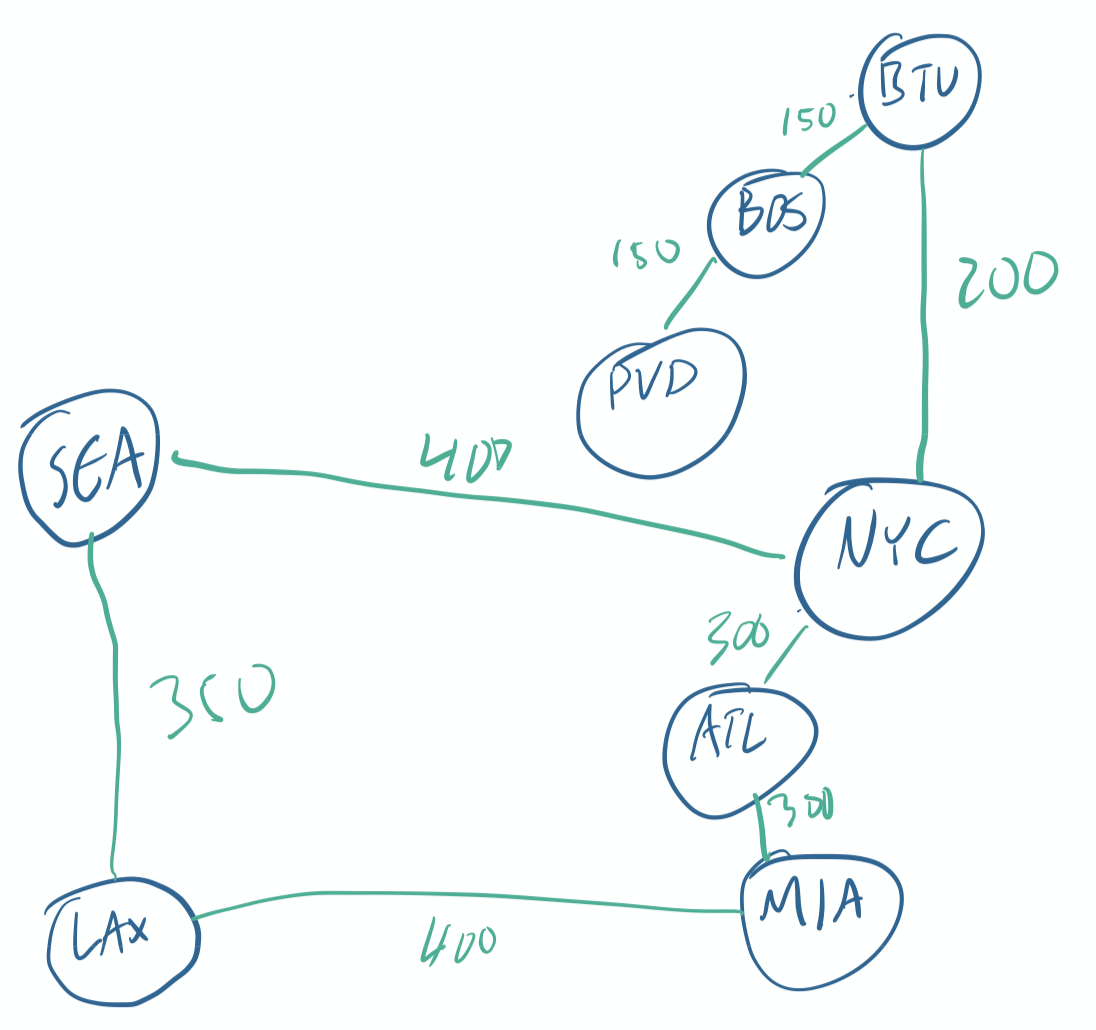
Distances and search in graphs
How would we determine how many flights it takes to get from Burlington (BTV) to Los Angeles (SEA)? It looks like it should take three flights: one from BTV to NYC, one from NYC to SEA, and one from SEA to LAX. But there are other possible paths: for instance, we could go BTV->NYC->ATL->MIA->LAX. We probably don’t want to do that–that’s a lot of stops! So maybe what we really want is the minimum number of flights.
Let’s start by solving an easier problem. Which airports can we get to from BTV in zero flights? Just one: BTV. I promise you, this is more useful than it sounds.
Now: which airports can we get to in one flight? By looking at the graph, it looks like we can get to NYC and BOS. In other words: in one flight, we can get to all of the airports that share an edge with the airports we could get to in zero flights.
Which airports can we get to in two flights? We can start with the airports we can get to in one flight, then look at all of their neighbors. We can get to PVD and BTV from BOS, and we can get to SEA, ATL, and BTV from NYC. We probably don’t want to include BTV in our list of airports we can get to in two flights–after all, we can get there in zero flights!
Finally, which airports can we get to in 3 flights? We can look at all of the airports from the previous step and then fly to their neighbors–but only the ones we haven’t examined yet. This gets us to MIA and LAX. So, now we know that it takes three flights to get to LAX.
An algorithm
How would we write a more formal description of this algorithm? As usual, we can start fairly informally and then refine.
function search(start, end):
distance to start = 0
to-visit = [start]
while nodes in to-visit:
node = first node from to-visit
for neighbor in neighbors:
if we haven't yet set neighbor's distance:
distance to neighbor = distance to node + 1
if neighbor == end:
return distance to neighbor
add neighbor to to-visit
This algorithm is an example of breadth-first search, which searches the nodes in a graph starting with those closest to a designated starting node.