CSCI 0050: Spellchecking, machine learning, and voting ... oh my! 8/1/19¶
Today was our last class!
Class overview:
- Python feature
global - How web abbs work
- Finish voting from yesterday
- Spell checker
- Machine learning
What is global?¶
We look at this in the context of the weather readings assignment.
In that assignment we looked at creating some list outside a function (ozone = []). We then defined a function register_data that added readings to ozone and SO2 lists. The outline looked something like the below:
ozone = []
def register_data(readings: List):
"""added readings to ozone and SO2 lists"""
.
.
.
ozone.append(r)
so2.append(r)
But when it came to testing, things became a little trickier. When we were writing our tests, we would define a function.
def test_register_data():
register_data(readings)
test(... on contents of ozone)
This created an issue if you ran your tests multiple times, as the test data could get cluttered up. One way we went about fixing this was to define an empty list inside the test_register_data function.
def test_register_data():
ozone = []
register_data(readings)
test(... on contents of ozone)
This worked, but sometimes you might want the things you did inside the register_data function to affect the ozone list. Additionally, we talked about when you define a function the defined "known names" get stuck in a temporary area. So, as our motivation question for talking about global: what if we wanted to reset the original ozone list before running our tests? What if we wanted to define a function that would reset our readings (call it reset_readings) that will set our readings back to a predefined state?
In Python, the way to do this is by using global. We can look at this in the context of defining reset_readings. The indicator global tells Python not make a new known name ozone in the temporary area, just use the one in the main area. This would look something like below:
def reset_readings():
global ozone
ozone = []
so2 = []
In the computer science world, the word that refers to the 'visibility' of variables (e.g. whether they've been defined in the temporary environment or not) is scoping.
Writing python code and putting it in the context of a web app¶
We next looked at how websites work.
When we talk about the web and web apps, we can talk about two different flavors:
- one that runs on the internet (web app)
- one that runs on a mobile/desktop (mobile/desktop app)
How do websites work, really?¶

First, we can consider a web page with an entry box and a submit button that gets displayed on your computer/browser. If you were to enter a number into the entry box, that is transmitted to another computer (called the server). This is where the code is run.
A message is sent over to the server that essentially says "run guess on input 5". The messages are a little more detailed than this, but for illustration purposes we will consider them like this.
On the webpage there will be a spot that says "I'm using guessing.py at kathi.com", where kathi.com is the name of the server. The message (run guess) gets sent to the server and the server will return a response. In this case, where the user guessed the wrong answer, the server at kathi.com will return a response that says "show to user "wrong answer try again"". The user's browser will then redraw the webpage to display a "wrong answer" message.
Getting a design to this is a little more complicated. We would need to learn to program in HTML and CSS. HTML will give your website structure, while CSS allows for design and layout (e.g. which font, which colors, and whether to stack things horizontally or vertically.
Finishing voting from yesterday¶
Yesterday, at the end of class, we were writing our results to .csv functions. We had shown how to open up a file on our computer and the idea of setting up a .csv writer.
from typing import List
import csv
def votes_for(name: str, votes: List[str]):
"""count number of times name is in the votes list"""
count = 0
for v in votes:
if v == name:
count = count + 1
return count
# we will continue this function tomorrow
votes = ["a", "b", "a", "a", "c", "d", "b"]
with open('election.csv', 'w', newline='') as csvfile:
# election.csv indicates the name of the new file
# 'w' indicates we will be writing to the file
# newline = '' indicates how we want to end a line
voteswriter = csv.writer(csvfile, delimiter = ',')
for cand in list(set(votes)):
# list(set(some_list)) == L.distinct(some_list) from Pyret
voteswriter.writerow([cand, votes_for(cand, votes)])
How many times are we going to have to process the voteslist?
$$\text{number of candidates} \times \text{number of votes}$$But remember that computer scientists tend to think of the worst case (just in case it happens!)
Here the worst case would be where we had some long list of candidates with one vote for each. The worst case could look like
$$\text{number of votes}^2$$Dictionaries¶
Is there a way to tally votes for all candidates in only one pass over the votes list?
Why yes, there is. The answer comes from last week — dictionaries!
A convenient way of improving this computation would use a two column table (Spoiler: this is actually just a dictionary).
| cand | tally |
|---|---|
| a | III |
| b | II |
| c | I |
| d | I |
We can rewrite our code to look like this!
# make a dictionary to tally the votes
tallies = {} # empty dictionary
for v in votes:
if v in tallies: # "is v a key in tallies dictionary?"
# if v already in dict, add one
tallies[v] = tallies[v] + 1
else:
# if not in dict, set it up!
tallies[v] = 1
with open('election.csv', 'w', newline='') as csvfile:
voteswriter = csv.writer(csvfile, delimiter = ',')
for cand in tallies:
voteswriter.writerow([cand, tallies[cand]])
Here we did linear work to set up our dictionary, then constant work to add to each candidate. Now our code runs linear in the # of votes.
Big O Notation¶
NB: This is optional, but interesting if you're intrigued by the idea of runnning time.
Computer scientists want to find an upper bound on the runtime. In most cases, we don’t have enough information about a program to say something as specific as “Every time the size of the input to my function increases by one, the function takes an extra five milliseconds to run.” Instead, we might be able to determine something a bit more general: “The runtime of the function varies linearly with the size of my input.”
For the math friendly folks, there's a convenient notation to rewrite the above sentence for the runtime of a function called "big O" notation.
$$ f \in O([k \rightarrow k])$$Where $k$ is the size of our input and $f$ is the function we’re describing. If you're interested in learning more (or think this notation looks cool), look here!
Making a spell checker¶
This example comes from this article by Brown alum Peter Norvig (now head of research at Google).
To make a spell checker, we need to tease out two problems.
- Is this a spelling error?
- What are viable selections?
If we were to think about a test word, Zebra, how could people misspell it?
- People could miss a letter: zbra, zera
- Add an extra letter: zeebra
- Hit a nearby key: zebta, zebr (hit caps lock)
- Transpose letter: zbera
When we're thinking about writing a spell checker, we don't have to start from nothing. People don't type completely random letters, we're starting from the kinds of mistakes that people might make — which actually gives us a lot of power. Given these known mistakes, we can actually generate possible misspellings of zebra as typed by people. Really what we're doing here is putting together a language model of the kinds of mistakes we're trying to catch.
Step 1: Misspellings¶
Our first step will be to generate this list of misspellings. We'll use a special feature of Python to look at substrings — the colon! This looks like below:
>>> "zebra"[2]
'b'
>>> "zebra"[:2]
'ze'
>>> "zebra"[2:]
'bra'
Python gives us the easy ability to take a word and split it at a particular position. If we're trying to generate misspellings of zebra, we can split it into two words (at position two) and do things like:
- zea + bra
- zeb + bra
- zec + bra
So let's think about turning this into a little bit of code:
def edits1(word):
"""all words that are a one-character edit from the given word"""
letters = 'abcdefghijklmnopqrstuvwxyz'
splits = [(word[:i], word[i:]) for i in range(len(word) + 1)]
return splits
edits1("zebra")
[(word[:i], word[i:]) for i in range(len(word) + 1)]
Where left of for indicates that we want to make a list of 'these values' and the right of for indicates we want to do this for each value of i.
For our spell checker, we need a list of all the possible deletions (of one character). We can take each pair from the above generated list and drop the first character from the second element of the pair.
def edits1(word):
"""all words that are a one-character edit from the given word"""
letters = 'abcdefghijklmnopqrstuvwxyz'
splits = [(word[:i], word[i:]) for i in range(len(word) + 1)]
deletes = [L + R[1:] for L, R in splits if R]
return deletes
edits1("zebra")
Now, if we wanted to insert a letter in:
def edits1(word):
"""all words that are a one-character edit from the given word"""
letters = 'abcdefghijklmnopqrstuvwxyz'
splits = [(word[:i], word[i:]) for i in range(len(word) + 1)]
deletes = [L + R[1:] for L, R in splits if R]
inserts = [L + char + R for L, R in splits for char in letters]
return inserts
# here we'll print out the first 5 so you get the idea, but there are a lot
edits1("zebra")[:5]
Now that we've built up this idea, we can see how Peter did it.
def edits1(word):
"All edits that are one edit away from `word`."
letters = 'abcdefghijklmnopqrstuvwxyz'
splits = [(word[:i], word[i:]) for i in range(len(word) + 1)]
deletes = [L + R[1:] for L, R in splits if R]
transposes = [L + R[1] + R[0] + R[2:] for L, R in splits if len(R)>1]
replaces = [L + c + R[1:] for L, R in splits if R for c in letters]
inserts = [L + c + R for L, R in splits for c in letters]
return set(deletes + transposes + replaces + inserts)
len(edits1("zebra"))
However, spell checkers often deal with two edits.
def edits2(word):
"""All edits that are two edits"""
return (e2 for e1 in edits1(word) for e2 in edits1(e1))
len(list(edits2("zebra")))
Now we can look at his whole file
import re
from collections import Counter
def words(text): return re.findall(r'\w+', text.lower())
WORDS = Counter(words(open('big.txt').read()))
def P(word, N=sum(WORDS.values())):
"Probability of `word`."
return WORDS[word] / N
def candidates(word):
"Generate possible spelling corrections for word."
return (known([word]) or known(edits1(word)) or known(edits2(word)) or [word])
def known(words):
"The subset of `words` that appear in the dictionary of WORDS."
return set(w for w in words if w in WORDS)
def edits1(word):
"All edits that are one edit away from `word`."
letters = 'abcdefghijklmnopqrstuvwxyz'
splits = [(word[:i], word[i:]) for i in range(len(word) + 1)]
deletes = [L + R[1:] for L, R in splits if R]
transposes = [L + R[1] + R[0] + R[2:] for L, R in splits if len(R)>1]
replaces = [L + c + R[1:] for L, R in splits if R for c in letters]
inserts = [L + c + R for L, R in splits for c in letters]
return set(deletes + transposes + replaces + inserts)
def edits2(word):
"All edits that are two edits away from `word`."
return (e2 for e1 in edits1(word) for e2 in edits1(e1))
# what's a possible candidate for the misspelling of "speling"
candidates("speling")
# what's a possible candidate for the misspelling of "seling"
candidates("seling")
Alright, we have a model for our language now. However, when autocorrect suggests a word it has to pick from a selection of potential options. To do this, we should also make a model of error which can take the frequency of use in real language.
def correction(word):
"Most probable spelling correction for word."
return max(candidates(word), key=P)
correction('korrectud')
He estimates that his checker is about 80% accurate. However, if we were to switch out his big.txt for some small text file small.txt with only "The quick brown fox jumps over the lazy dog" in it, we get different behavior.
WORDS = Counter(words(open('small.txt').read()))
candidates("speling")
candidates("quck")
This should give you the sense that some of the things that computers and programs do don't just lie in the programs, they also rely on the data. The idea of figuring out what set of data will make your tools work effectively is a big part of making computational tools work best for you.
Machine Learning¶
(The fruit example is from Professor Michael Littman's CS8 lecture notes)
Machine learning is looking for patterns in data to help us make decisions.
Let's say we have the task of training a computer to recognize pictures of apples and strawberries. What might distinguish an apple from a strawberry?
- Shape
- Size
- "Redness"
When you have something that you want a computer to recognize, you have to think of features. For this thought exercise, we will think of redness and size.
We'll start with a set of pictures that we know are apples or strawberries. We can think about plotting this on a two dimensional plane with size on one axis and "redness" on another. We can plot data on apples and strawberries on this plane and use statistics to plot a line that separates apples and strawberries.
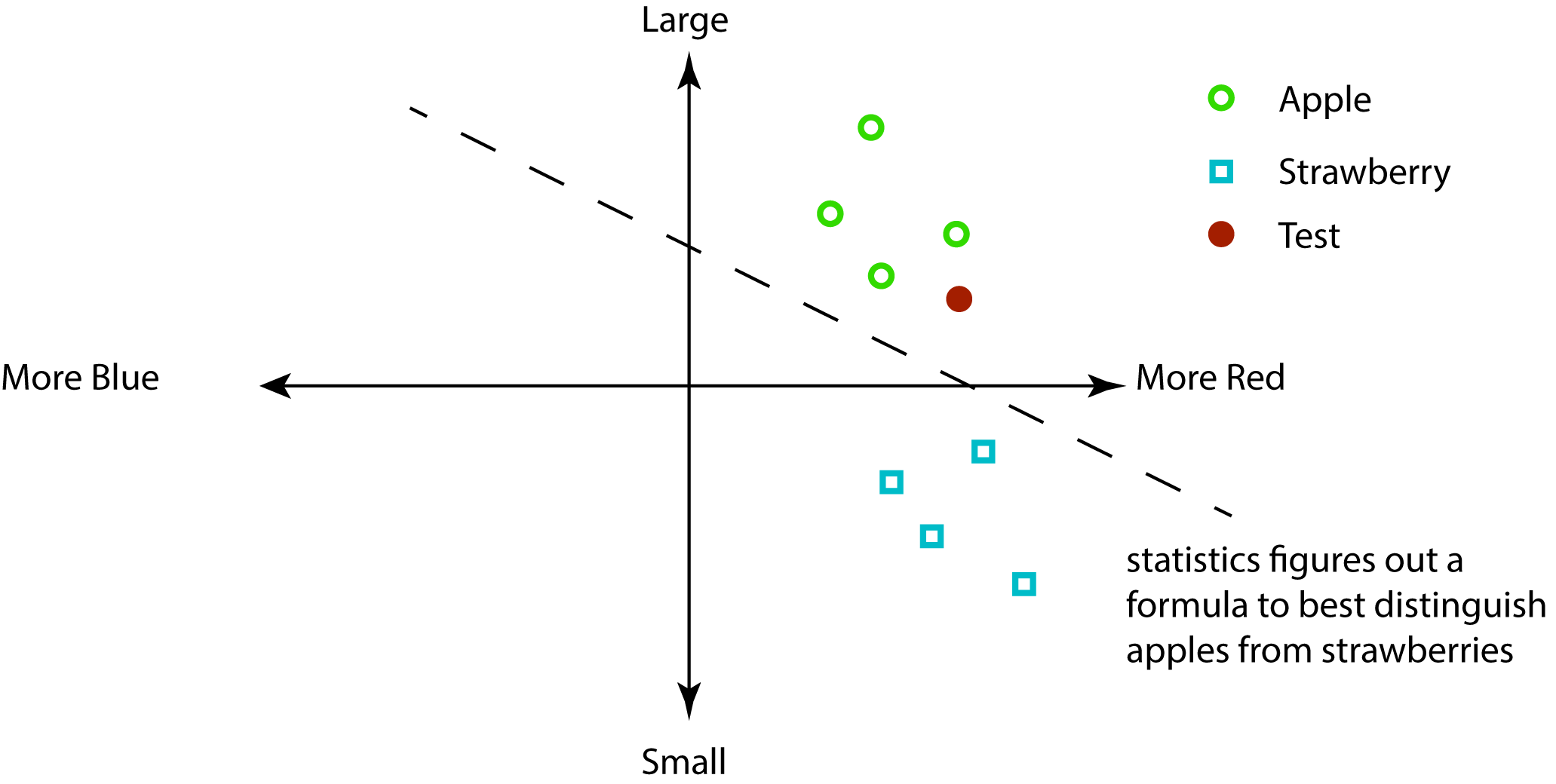
What can go wrong?¶
Well this looks innocuous... What could go wrong?
- Your training data is uesd to train the model. If you have bad data in, you will get bad data out. If you have biased data in, you will get biased data out.
- Models lack transparency. If you got a bad score on a parole granting machine learning model, models lack the ability to provide a rationale for the decision (see FAT machine learning).
Suggested reading: Weapons of Math Destruction by Cathy O'Neill