|
Planar
graphs
arise in applications such as road map
navigation and logistics, graph drawing, and
image processing. In this course, we study algorithmic techniques that exploit planarity in
addressing classical problems, e.g. Traveling
Salesperson, Shortest Paths,
and Maximum Flow.
Prerequisite: CS 157 or
equivalent (introductory algorithms)
Focus
The focus is on algorithms for addressing logistics and planning problems in road maps.
Textbook
Draft
textbook chapters available at http://planarity.org
(to be updated as the class proceeds).
Work
Homeworks will be assigned once every week or two for the first
three-fourths of the semester. During the last
one-fourth of the semester, students will work on
projects. In addition, there will likely be a
midterm to ensure students have mastered the
basics. Class participation will also affect
students' grades.
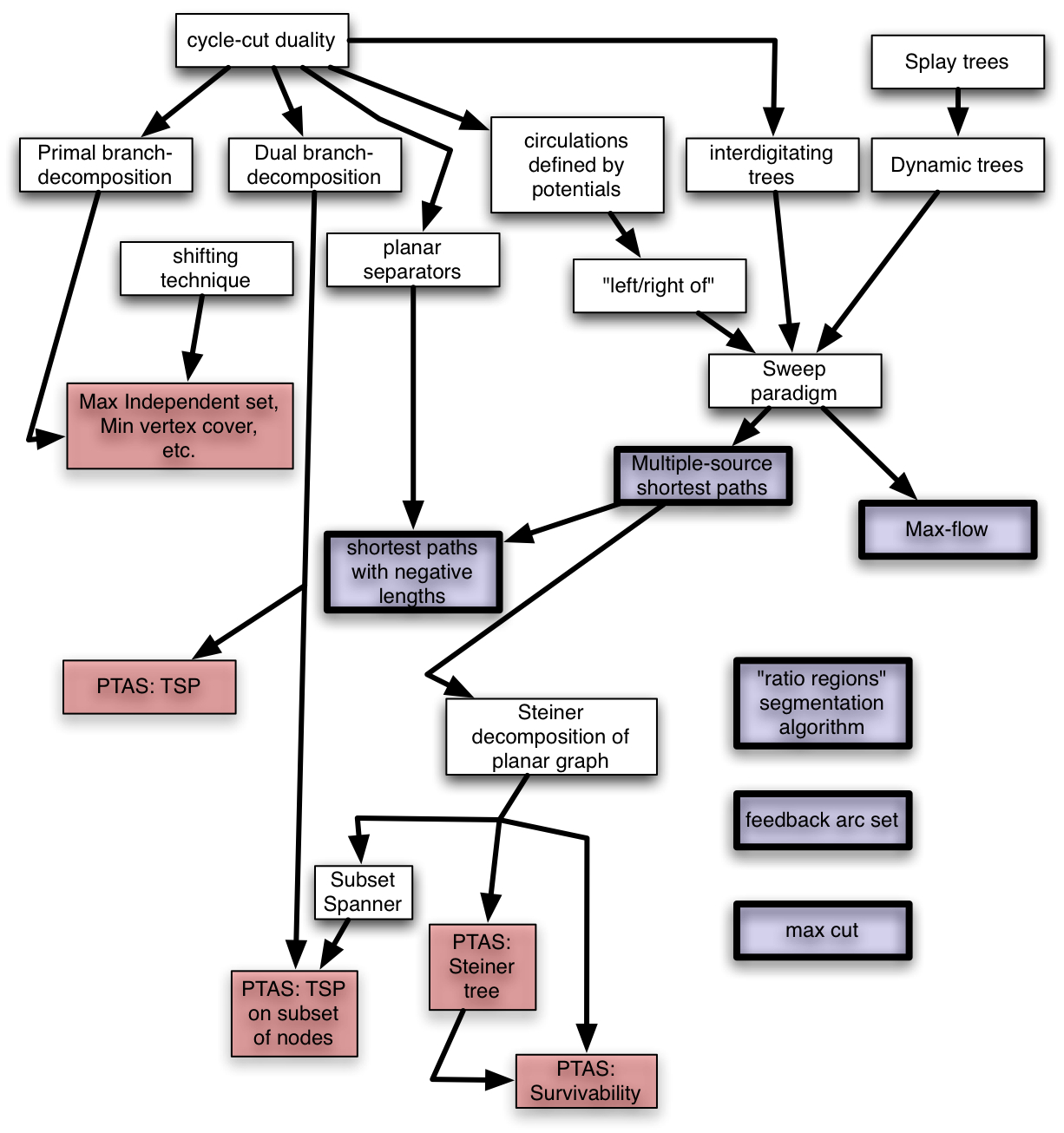
Topics will be chosen from among the following
- Separators in trees
- Elementary graph theory
- Embedded graphs and duality
- Planar graphs and planar duality
- Maintaining a bounded-outdegree orientation
- Separators in planar graphs
- Primal-dual method for approximation
- Approximation algorithms for vertex-weighted Steiner trees and
feedback vertex set
- Carvingwidth and branchwidth
- Optimization algorithms for graphs with bounded branchwidth
- Brenda Baker's method for approximation schemes
- Metric version of Baker's method, and approximation for {\em
$k$-center}/{\em $r$-domination}
- Linear-time approximation scheme for traveling salesperson problem
- Brick decomposition and approximation scheme for Steiner
traveling salesperson problem
- Approximation scheme for Steiner tree
- Prize-collecting clustering
- Approximation scheme for Steiner forest
- Bicriteria approximation scheme for bisection
- Maximum flow in directed $st$-planar graphs
- Shortest paths with nonnegative edge-lengths
- Dynamic-tree data structure
- Maximum flow in directed planar graphs
- Multiple-source shortest paths
- Maximum flow and multiple-source shortest paths in graphs with
small weights
- Fast construction of brick decomposition
- Shortest paths in directed graphs with positive and negative edge-lengths
- Approximate distance oracle
- Fakcharoenphol-Rao priority queue
- Exact distance oracle
- Multiple-source multiple-sink maximum flow
 |
|
|