Oracle

1. Topological Sort

A topological sort finds a linear ordering of vertices in a simple, directed acyclic graph G = (V, E), such that for all edges (u, v) in E, u precedes v in the ordering.

For example, the order of formula cell evaluation when recomputing formula values in spreadsheets is an application of topological sort. Another example is to determine the order in which a student can take classes given a list of prerequisites. Depending on the graph, many valid topological sorts may exist for each of these problems.

2. The Assignment

You will write two programs for this assignment: a topological sorting program (named topsort) and an oracle (named oracle).

Implement the topological sorting program using the following pseudocode:

function topsort(g): // g = directed acyclic graph
    L = empty list to store ordering
    S = set of vertices with no incoming edges
    while S is not empty:
        u = vertex removed from S
        append u to L
        for each vertex v where edge e = (u,v) in g:
            remove e from g
            if v has no other incoming edges in g:
                insert v in S
    return L

Your program should adhere to the input-output specification in Part 3 of this assignment.

Being confident in your software's correctness involves more than just writing code and some unit tests. Methods of proving correctness exist and will be explored later in the course, but most computer scientists and software companies rely on automated testing to demonstrate correctness. For this assignment, you will build an automated testing oracle for topological sorting programs.

Your oracle will consume the path of a topological sorting program and the number of inputs to generate, n. Then, your oracle will generate n valid inputs and write each of them to the provided program's standard input. Your oracle will check that each output is in fact a topological sort of the corresponding input and conforms to the specifications in Part 3 of the assignment.

If the provided program always produces a valid topological sort (up to some value of "always"), then your program should exit with status 0. Otherwise, your program should exit with status 1. The oracle should not write anything to standard output or standard error. Note that you may assume n is valid (a non-negative integer) and all input is well-formed.

Using your oracle, check that your implementation is correct.

You are allowed to use any programming language to implement topsort and oracle for this assignment, but they need to conform the input-output specification (see next section), so the programs need to be executable on the department machines and be able to read from standard input. That means you can't use languages like Scratch or Pyret. If you need to compile files, you should do so on the department machines or via ssh because binaries that work on your computer might not work on department machines. If you don't have a strong preference, we suggest you use Python. See Part 5 for more information.

3. Input-Output Specification

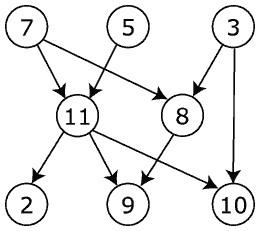
Consider the following directed acyclic graph (DAG):

The topological sorting programs consumed by your oracle, including your own topsort, will read a directed acyclic graph from standard input in the following form:

  7 11
  7 8
  3 10
  5 11
  3 8
  8 9
  11 10
  11 2
  11 9

where each line represents a directed edge with each vertex name, an alphanumeric, case-sensitive string of any length, separated by a space (in the example of 7 11, vertex 7 comes before 11). Note that the order of lines does not matter. And remember, a valid input should not have cycles!

The programs should write standard output of the following form:

  3
  5
  7
  11
  8
  9
  10
  2

where each line containts a vertex name in topological order from top to bottom. Recall that for valid inputs, your program should exit with status 0, and nothing should be printed to standard error.

4. Testing

To test your oracle, try running it on Unix's topological sorting program included on all department machines:

./oracle /usr/bin/tsort n

where n is the number of inputs to generate. Your oracle should exit with status 0 on this program. To ensure your oracle detects incorrect topological sorting programs, try running it on deliberately broken implementations of your creation. Your oracle should exit with status 1 on these broken programs. Detecting incorrect implementations is just as important as detecting correct implementations! Note that we will not test your program against a topological sorting program that does not terminate.¹

5. Lab

We'll offer an optional lab on Python, focusing on implementing file input/output necessary for this assignment. We encourage everyone to come, especially those unfamiliar with file input/output. We will send an email with the location and time of the lab.

6. Handing In

Run cs1950y_handin oracle from a directory holding your topological sorting program (named topsort) and oracle (named oracle), and any additional files you wish to submit. If your topsort and oracle are binaries, you need to include the source code as well. You should receive an email confirming that your handin has worked.

If you are not registered, you will not be able to run the above handin script. Please zip your files, name it oracle.zip, and send it to us at cs1950ytas@lists.brown.edu. Please only do so if you cannot register for the course by the due date of the assignment.

[1]: Testing whether a program terminates is impossible due to the Halting problem. Most oracles work around this by setting a threshold (e.g., 3 minutes). If the tested program does not terminate within the threshold, the program is considered to be non-terminating and its process therefore could be killed. However, you need not to implement the check for this assignment.