PB (meaning 'probability of boundary') is the relatively new boundary detection algorithm that performs better than the classical sobel and canny methods, as pb takes into account texture gradients in detemining the boundary of an element in an image. While the classical algorithms tend to output false positives for object boundaries when dealing with a textured object, pb is able to smooth out the effects of these textures, returning a more accurate delination of the pictured object.
The first step in the pb algorithm is to create a texton map, where textons are discrete texture elements generated by clustering filter bank responses. So, the real fist step is to generate the filter bank that will produce these responses. My filter bank consists of 16 orientations for two filter sizes (sigma = 1 and sigma = 2). For each size (sigma) the bank is created by convolving a gaussian filter with a sobel filter, and then rotating the result. See the filter bank below:

Once this filter bank has been generated, (in this case the bank has 32 filters), the original image (grayscaled) is filtered with each one to create 32 'filter responses,' which corresponds to a size-32 vector of responses for each pixel. To generate the texton map, we use the kmeans algorithm to cluster the response vectors in order to return a (scalar) texton id. In my implementation, I used k = 32, which means that in the texton map, each pixel fell into one of 32 texture categories.
The next step is to use this texton map, as well as a greyscale version of the image, to create gradients for texture and brightness, respectively. The gradients are produced by comparing distributions of values that fall into a certain range (histograms) that in turn lie in left/right half-disc pairs. In my implementation, I use 3 sets of half disc pairs, with radii 5, 10, and 15, and 8 orientations each, for a total of 24 pairs. See below:

Then the algorithm for computing the gradient response for each scale and each orientation is as follows (same as handout):
for i=1:num_bins
tmp = 1 where img is in bin i and 0 elsewhere
g_i = convolve tmp with left_mask
h_i = convolve tmp with right_mask
update chi_sqr_dist
end
In my implementation, k=32 bins are used in calculating both the texture gradient and the brightness gradient. The above alogrithm creates a texture and brightness gradient response for each half-disc pair for each pixel. In this case, much like in the creation of the texture response, this means there is a size-32 vector associated with each pixel both for texture gradient and brightness gradient.
Finally, these gradient response vectors are each averaged and then added together to compress the responses into a picture-sized 2D gradient response map. To obtain our final pb-edge image, the classcical canny edge detection result is multiplied by this response map and then normalized. See below for the performance of this result compared to sobel and canny baselines (as they are compared to human-prodcuded 'ground truth' edges):
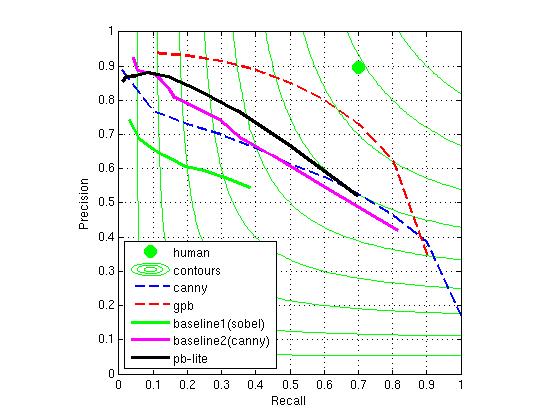
Although there's a little funkiness with canny continuing to beat the pb-lite result when Recall is less than 0.1, it's clear that in general pb completely outperforms both classical edge detection methods.