Suppose Alice and Bob wish to select a secret key to facilitate their
private communication over an insecure network. We assume the value
of the modulus m is known to everyone in
the network. Alice privately selects a large random number A, and
calculates 
using the repeated squaring algorithm.
We will call the resulting number AlicePart because it is her
contribution to the selection of the shared key. She sends
AlicePart to Bob. Similarly, Bob privately selects a large random
number B, and calculates 
, which we will call
BobPart. He then sends BobPart to Alice.
Now the parties can calculate their shared key. Alice privately calculates her key by raising BobPart to the power of A, using modular arithmetic. Similarly, Bob calculates his key by raising AlicePart to the power of B, again using modular arithmetic. Because of the property of exponentiation described above, the key Alice calculates and the key Bob calculates are the same number, as we now show:
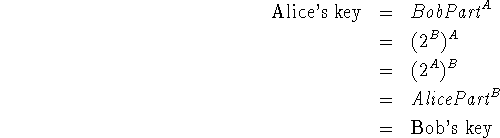
Thus the two parties now have a common key and can preserve their privacy while communicating over the insecure network, using, say, a traditional one-key cryptosystem.