

|
People like choices. We like to have different ways of solving the same problem, so that we can explore different trade-offs and efficiencies. This chapter is devoted to the exploration of different ways of solving a problem we \fix{discussed}{discuss} in an earlier chapter--the implementation of an ordered dictionary. Namely, we study several alternative data structures based on trees for realizing ordered dictionaries. We begin this chapter by discussing binary search trees, and how they support a simple tree-based implementation of an ordered dictionary, but do not guarantee efficient worst-case performance. Nevertheless, they form the basis of many tree-based dictionary implementations, and we discuss several in this chapter. One of the classic implementations is the AVL tree, which is a binary search tree that achieves logarithmic-time search and update operations. We also introduce the concept of a multi-way search tree, which is an ordered tree where each internal node can store several items and have several children. A multi-way search tree is a generalization of the binary search tree, and like the binary search tree, it can be specialized into an efficient data structure for dictionaries by imposing additional constraints. One of the advantages of using these multi-way trees is that they often require fewer internal nodes than binary search trees to store items. But, just as with binary search trees, multi-way trees require additional methods to make them efficient for all dictionary methods. We discuss a specific multi-way tree, the (2,4) tree. This is a multi-way search tree, such that all the external nodes have the same depth and each node stores 1, 2, or 3 keys and has 2, 3, or 4 children, respectively. The advantage of this kind of trees is that it has algorithms for inserting and removing keys that are simple and intuitive. Update operations rearrange a (2,4) tree by means of natural operations that split and merge `nearby' nodes or transfer keys between them. A (2,4) tree storing n items uses O(n) space and supports searches, insertions, and removals in logarithmic worst-case time. We present red-black trees, as well. These are binary search trees whose nodes are colored `red' and `black' in such a way that the coloring scheme guarantees logarithmic height. There is a simple, yet illuminating, correspondence between red-black and (2,4) trees. Using this correspondence, we motivate and provide intuition for the somewhat more complex algorithms for insertion and removal in red-black trees, which are based on rotations and recolorings. Like an AVL tree, a red-black tree uses linear space and supports searches, insertions, and removals in logarithmic worst-case time. The advantage that a red-black tree achieves over an AVL tree is that it can be restructured after an insertion or removal with only constant number of rotations (although at the expense of more complex operations). Finally, we discuss external searching, that is, searching in external memory (which will usually be a disk). We introduce a type of multi-way tree called the B-tree and we show how it can be used to store and search items so as to minimize the number of input-output (I/O) operations. There are admittedly quite a few kinds of search trees discussed in this chapter, and we recognize that a reader or instructor with limited time might be interested in studying only selected topics. For this reason, in the figure below, we show the conceptual dependencies between the sections in this chapter. Thus, for example, a reader can focus on binary search trees and then study AVL trees, (2,4) trees (possibly along with red-black trees as well), and/or external searching. 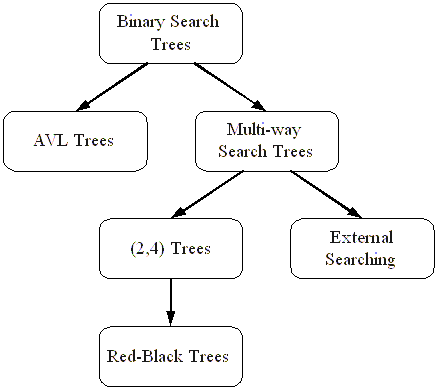
|