
Project 2: Image Blending
Seamless image blending using poisson equation solving
(Pérez, et al.).
Due Date: 11:59pm on Wedbesday, February 17th, 2010
Brief
- This handout: /course/cs195g/asgn/proj2/handout/
- Stencil code: /course/cs195g/asgn/proj2/stencil/
- Data: /course/cs195g/asgn/proj2/data/
- Handin: cs195g_handin proj2
- Required files: README, code/, html/, html/index.html
Requirements
You are required to implement a poisson image blending as well as take your own photos and apply your algorithm to those images to get full credit.
Details
MATLAB stencil code is available in /course/cs195g/asgn/proj2/stencil/. You're free to do this project in whatever language you want, but the TAs are only offering support in MATLAB. One file supplied is fiximages.m which automatically resizes and moves all the images so that one could easily composite them. The stencil code is set up to do this immediately. Feel free to use or ignore this function. Another file getmask.m will allow you to interactively make an image mask.
You should take a look at Pérez, et al., especially section 2: "Discrete Poisson solver", before trying to implement the algorithm. It explains the algorithm in better detail than this handout will.
The algorithm boils down to this: for each pixel under the mask, it's value satisfies the equation:
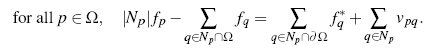
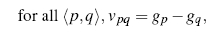
- f* = source image
- g = target image
- p = pixel
- Ω = pixels under the mask
- ∂Ω = pixels who have at least one neighbor under the mask
- Np = neighborhood of pixel p
- fp = new value of pixel p (the value you are solving for)
- f*p = value of pixel p in in the source image
- vpq = gradient of the pixel to a neighbor in the source image g
If you were to look at the equation as just solving for fp, you would see that the equation simplifies to the new pixel value equals the average of it's neighborhood plus the gradient of the pixel to it's neighbors. Notice that the value taken for the neighbor is the new value (fq) if the neighbor is under the mask and it is the target image value otherwise. Since the new (unknown) pixels may have neighbors who are also unknown, you can think of the problem recursively or as a large series of constraints. Each pixel in the target image is assigned a variable, P1,1, P1,2, P1,n, P2,1,..., through Pm,n for an m by n image. Thus, the constraints put on the variable Pi,j are:
- If Pi,j ∉ Ω, Pi,j = Targeti,j
- Otherwise:
(# of neighbors) * Pi,j =
sum for each connected neighbor Q: (i-1,j), (i+1,j), (i,j-1), (i,j+1)
if Q is under the mask,
+QUnknown
else
+QTarget
end
+(PSource - QSource)
The above constraints yield m*n linear equations with m*n unknowns. which can be represented in the standard matrix form Ax = b and solved to get exactly one solution. Here P is a column vector comprised of the m*n variables (pixels) in the final image, A is composed of the constraint equations listed above and b is a combination of known pixel values and calculated values.
The coefficient matrix will be mostly sparse since the only pixels affecting the output value are the given pixel and 4 of it's neighbors. (Hint: use a sparse matrix). Also instead of using inv(A) in Matlab to solve Ax=b, use: x = A\b; where A is the coefficient matrix, b is the solution vector, and x is the output values for the pixels. If you don't, you might get annoying errors that make no sense.
Write up
For this project, just like all other projects, you must do a project report in HTML. In the report you will describe your algorithm and any decisions you made to write your algorithm a particular way. Then you will show and discuss the results of your algorithm. Also discuss any extra credit you did. Feel free to add any other information you feel is relevant.
Extra Credit
You are free to do whatever extra credit you can think of. Here are some suggestions:
- Mixing Gradients to allow transparent images or images with holes (from the paper)
- Automatically shifting the offset of the source image to decrease the difference of the images in the composite area
- Implement and compare other blending techniques, such as Laplacian pyramid blending
- Experiment with other heuristics and metrics, such as down-weighting areas of high gradient in the source image
Graduate Credit
To get graduate credit on this project you must do one form of extra credit of sufficient difficulty. Any one of the suggested extra credit satisfies this requirement.
Handing in
This is very important as you will lose points if you do not follow instructions. Every time after the first that you do not follow instructions, you will lose 5 points. The folder you hand in must contain the following:
- README - text file containing anything about the project that you want to tell the TAs
- code/ - directory containing all your code for this assignment
- html/ - directory containing all your html report for this assignment (including images)
- html/index.html - home page for your results
Then run: cs195g_handin proj2
If it is not in your path, you can run it directly: /course/cs195g/bin/cs195g_handin proj2
Rubric
- +70 pts: Seamless image blending implementation
- +10 pts: Using at least 5 images you have taken
- +20 pts: Write up
- +20 pts: Extra credit (up to twenty points)
Final Advice
- A naive implementation will run slowly because of indexing into a sparse matrix. Test your algorithm on smaller images first.
- That part of the algorithm can be made significantly faster by finding all the coefficient matrix values ahead of time and then constructing the sparse matrix; see sparse(i,j,s,m,n,nzmax)
- Helpful matlab commands that may help you speed up your algorithm: find, sort, diff, cat, sparse, spy
- The TAs are fully aware of the implementations available on the internet, we'll know if you used them.
Credits
Project derived from Poisson Image Editing