
From left to right: (1) input image (2) boundary strength from baseline method based on Canny edge detection (3) sample "pb-lite" result (4) gpb (state of the art). Notice that texture edges are less likely to be mistaken for boundaries by (3) and (4).
Project 2: pb-lite: Boundary Detection
CS 143: Introduction to Computer Vision
Brief
- Stencil code: /course/cs143/asgn/proj2/stencil/
- Data: /course/cs143/asgn/proj2/data/
- Handin: cs143_handin proj2
- Required files: README, code/, html/, html/index.html
- Due date: Monday, Oct 10th, 11:59pm
Starter Code
The starter code provides a outline of the pipeline and handles image loading, saving, visualization, and most significantly quantitative evaluation. The starter code will quantify the performance of your boundary detector on a subset of the human-annotated BSDS500 dataset. The evaluation process is non-trivial and calls mex-compiled code. We have precompiled this code for Linux (32 and 64 bit) and MacOS (64 bit). The code seems difficult to compile for Windows platforms although you are welcome to try and let us know if you have success. The code can be compiled by calling proj2/stencil/bench/source $ source build.sh from your shell or running build.m from the same directory in Matlab. The starter code provides a baseline boundary detector based on the average of Canny edge detection with different parameter settings. This is a non-trivial baseline, but you can beat it!
Overview
Boundary detection is an important, well-studied computer vision problem. Clearly it would be nice to have algorithms which know where one object stops and another starts. But boundary detection from a single image is fundamentally difficult. Determining boundaries could require object-specific reasoning, arguably making the task "vision hard".
Classical edge detection algorithms, including the Canny and Sobel baselines we will compare against, look for intensity discontinuities. The more recent pb boundary detectors significantly outperform these classical methods by considering texture and color gradients in addition to intensity. Qualitatively, much of this performance jump comes from the ability of the pb algorithm to suppress false positives that the classical methods produce in textured regions.
In this project, you will develop a simplified version of pb, which finds boundaries by examining brightness, color, and texture information across multiple scales. The output of your algorithm will be a per-pixel probability of boundary. Several papers from Berkeley describe their algorithms and how their methods evolved over time. Their source code is also available for reference (don't use it). Here we investigate a simplified version of the recent work of Arbelaez, Maire, Fowlkes, and Malik. TPAMI 2011 (pdf). Our simplified boundary detector will still significantly outperform the well regarded Canny edge detector. Evaluation is carried out against human annotations (ground truth) from a subset of the Berkeley Segmentation Data Set 500 (BSDS500)
Details
The main steps in Arbelaez et al. 2011 are:
- Low-level feature extraction: (1) brightness, (2) color, and (3) textons
- Multiscale cue combination with non-maximum suppression
- Spectral clustering
The focus of pb-lite will be on the representation of brightness, color and texture gradients (bullet point 1). This is covered (briefly) in Section 3.1 of Arbelaez et al. 2011. We will trivialize the multiscale cue combination. We will get a simple form of non-maximum suppression by combining our pb-lite estimates with a classical edge detector. We will skip spectral clustering. You will implement the following pipeline:
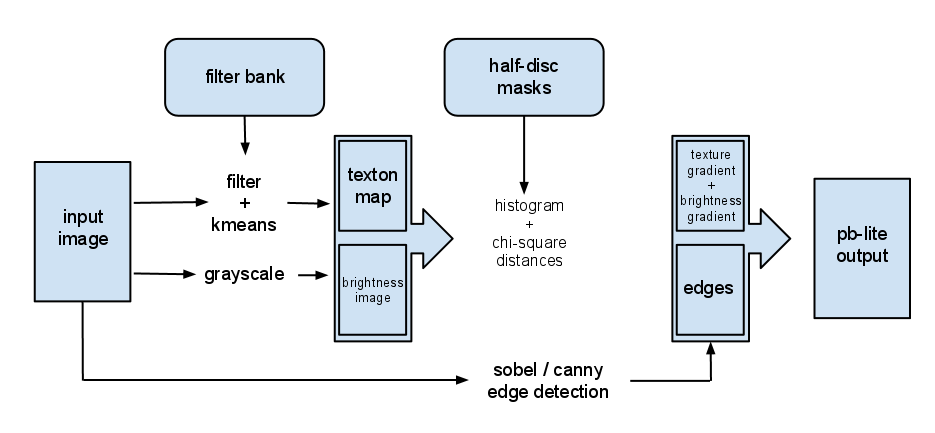
The major steps are to pre-define:
- a filter bank of multiple scales and orientations.
- half-disc masks of multiple scales and orientations.
and then for every image:
- create a texton map by filtering and clustering the responses with kmeans.
- compute per pixel texture gradient (tg) and brightness gradient (bg) by comparing local half-disc distributions.
- output a per-pixel boundary score based on the magnitude of these gradients combined with a baseline edge detector (Canny or Sobel).
Finally the output for all of the evaluate using the the Berkeley Segmentation Data Set 500 (BSDS500) (code already provided)
Texture Representation
The key distinguishing element between pb-lite and classical edge detection is the ability to measure texture gradients in addition to intensity gradients. The texture gradient at any pixel should summarize how quickly the texture is changing at that point. The key technical challenges are how to represent local texture distributions and how to measure distances between them. As in pb, we will represent texture as a local distribution of textons, where textons are discrete texture elements generated by clustering filter bank responses. Texture and brightness gradients will be measured by comparing the distributions of textons or brightnesses within half-discs centered on a pixel of interest.
Filter Bank and Half-disc Masks
Filtering is at the heart of building the low level features we are interested in. We will use filtering both to measure texture properties and to aggregate regional texture and brightness distributions. There are two sets of filters in this project. The first is an oriented filter bank for computing the textons. A simple but effective filter bank is a collection of oriented derivative of Gaussian filters. These filters can be created by convolving a simple Sobel filter and a Gaussian kernel and then rotating the result. Suppose we want o orientations(from 0 to 360 degrees) and s scales, we should end up with a total of o*s filters. A sample filter bank of size 16 x 2 is shown below:

The half-disc masks are simply (pairs of) binary images of half-discs. These very important because it will allow us to compute the chi-square distances using a filtering operation, which is much faster than looping over each pixel neighborhood and aggregating counts for histograms. Once you get the above filter bank right, forming the masks will be trivial. A sample set of masks (8 orientations, 3 scales) is a shown below:

The filter banks and masks only need to be defined once and then they will be used on all images. You have some discretion to experiment with different filter banks and masks. You can earn extra credit by trying richer sets of filters and masks.
Hint: some useful Matlab functions include: fspecial, imrotate, conv2, imfilter, cell, reshape.
Generating a Texton Map
Filtering an input image with each element of your filter bank results in a vector of filter responses centered on each pixel. For instance, if your filter bank has 16 orientations and 2 scales, you would have 32 filter responses at each pixel. A distribution of these 32-dimensional filter responses (E.g. all of the vectors in an image region) could be thought of as encoding texture properties. We will simplify this representation by replacing each 32-dimensional vector with a discrete texton id. We will do this by clustering the filter responses at all pixels in the image in to K textons using kmeans (kmeans code is provided). Each pixel is then represented by a one dimensional, discrete cluster id instead of a vector of high-dimensional, real-valued filter responses. This can be represented with a single channel image with values in the range of [1, 2, 3, ... , K]. K=64 seems to work well but feel free to experiment. To visualize the a texton map, you can try imagesc(tmap);colormap(jet);
Local Texton Distributions
We will represent local texture distributions by building K-dimensional texton histograms over regions of interest. These histograms count how often each texton is observed. The regions of interest we will use are the half-disc masks previously discussed.
Analogous local histograms could be built for brightness or color, after brightness and color have been quantized in to some number of clusters.
Computing Texture Gradient and Brightness Gradient
The local texton gradient (tg) and brightness gradient (bg) encode how much the texture and brightness distributions are changing at a pixel. We compute tg and bg by comparing the distributions in left/right half-disc pairs centered at a pixel. If the distributions are the similar, the gradient should be small. If the distributions are dissimilar, the gradient should be large. Because our half-discs span multiple scales and orientations, we will end up with a series of local gradient measurements encoding how quickly the texture or brightness distributions are changing at different scales and angles.
We will compare texton and brightness distributions with the chi-square measure. The chi-square distance is a frequently used metric for comparing two histograms. It is defined as follows:
chi_sqr(g,h)=.5*sumi=1:K( (gi-hi)2 / (gi+hi) ), where g and h are histograms with the same binning scheme, and i indexes through these bins. Note that the numerator of this expression is simply the sum of squared difference between histogram elements. The denominator adds a "soft" normalization to each bin so that less frequent elements still contribute to the overall distance.
To efficiently compute tg and bg, filtering can used to avoid nested loops over pixels. In addition, the linear nature of the formula above can be exploited.
Suppose we have a function get_gradient(img,masks,bins), where img is a single channel image of discrete values, such as a texton map. At a single orientation and scale, we can use
a particular pair of masks to aggregate the counts in a histogram via a filtering operation, and compute the chi-square distance (gradient) in one loop over the bins according to the following outline:
chi_sqr_dist=img*0
for i=1:num_bins
tmp = 1 where img is in bin i and 0 elsewhere
g_i = convolve tmp with left_mask
h_i = convolve tmp with right_mask
update chi_sqr_dist
end
The above procedure should generate a 2D matrix of gradient values. Simply repeat this for all orientations and scales, you should end up with a 3D matrix of size n*m*(o*s), where n, m are dimensions of the image.
Hint: you might want less than 256 bins when computing bg.
Output pb-lite
The final step is to combine information from the features with a baseline method (based on Sobel or Canny edge detection). The magnitude of the features represents the strength of boundaries, hence, a simple mean of the feature vector at location i should be somewhat proportional to pb. Of course, fancier ways to combine the features can be explored for better performance and extra credit. As a starting point, you can simply use an element-wise product of the baseline output and the mean feature strength to form the final pb value, this should work reasonably well.
Evaluating Boundary Detection
The goal of this project is to have a boundary detector that beats the baseline method provided, which is based on Sobel/Canny edge detection. The evaluation is based human annotation (groundtruth), collected as part of the BSDS500 dataset. A detailed description of the evaluation scheme is presented in Arbelaez et al. 2011 (pdf). A good performance measure is the F score of the precision-recall curve. The stencil code does automatic evaluation for you. A sample precision-recall curve is shown below:
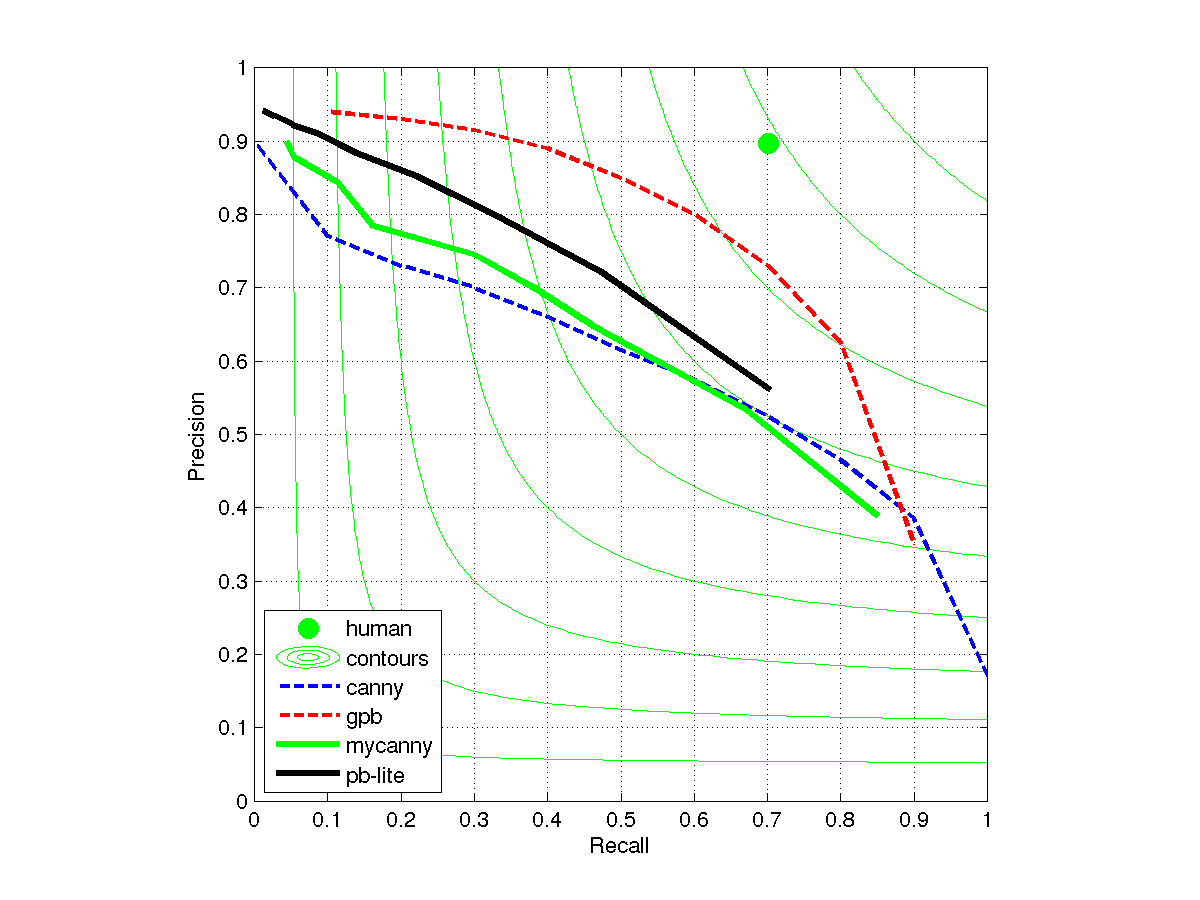
(dotted lines are copied from figure 17 in Arbelaez et al. 2011 (pdf), solid lines come from actual implementations in MATLAB)
The above diagram is generated using all of the 200 test images in the dataset. If you are using a subset of the testset, you might get better/worse performance because some images are "easier" or "harder". But if you do better than gpb (dotted red line), something is either wrong or you can publish a top paper.
Extra Credit Suggestions
This project has many opportunities for deeper exploration. For instance, one could implement some of the more complex strategies of Arbelaez et al. 2011 (pdf) which have been simplified for the base requirements. You are free to try any extensions you can think of and we may find them worthy of extra credit, especially if you can show quantitative improvement in performance. In particular, the student or students (in case of tie) who achieve the best ODS F-score on the full 200 image test set will get recognition and extra credit.
Below are several specific extra credit suggestions:
- up to 5 pts: Use richer filter banks beyond oriented derivatives of Gaussians. For instance, add center-surround filters or more orientation selective filters.
- up to 5 pts: Use richer masks to aggregate local texton, brightness, or color distributions. The masks do not necessarily need to be binary or circular. Each additional mask (pair) gives you an additional gradient measurement.
- up to 5 pts: Use richer features beyond the required tg and bg, such as color features.
- up to 5 pts: Use integral images (a.k.a. summed area tables) to quickly compute local histograms. Refer to the appendix in Arbelaez et al. 2011 (pdf). This will not increase boundary detection accuracy but could provide a speed up.
- up to 10 pts: The mapping from filter responses to textons does not need to be discrete. One can use "soft assignment" to have each filter response cast a weighted vote for multiple textons (e.g. at this pixel, it seems 70% like texton 14, 20% like texton 55, and 10% like texton 42). This will require you to change the pipeline because the notion of a discrete, scalar texton map is no longer applicable. There are several other more complex strategies in the spirit of soft assignment to map from feature vectors to histograms (See this recent survey).
- up to 10 pts: Use Earth Mover's distance to compare histogams rather than chi-square distance. For the full points you must do this for both brightness and texture features. For the texture features one must determine a meaningful distance between each histogram bin. You are free to use existing code for the actual EMD computation (E.g. this code).
- up to 15 pts: Instead of going from oriented, multiscale gradients to pb by averaging gradient magnitude, instead learn the relationship between gradient values and boundary likelihood using the BSDS training set. For instance, one could train an SVM which takes texture, brightness, and color gradients, as well as canny edge response, and classifies each pixel as boundary or non-boundary. This strategy has been used in the literature, but our experiments suggest that the gain is small because the mapping between gradients and boundary likelihood is, in fact, quite simple (more gradients mean more likelihood of boundary). To make this strategy really worthwhile one might need to change the pipeline so that the learning algorithm can directly observe the texture distributions, although this may require switching to a universal texton dictionary. You are free to use any existing machine learning code.
Graduate Credit
To get graduate credit on this project you must do 10 points worth of extra credit. Those 10 points will not be added to your grade, but additional extra credit will be.
Writeup
For this project, and all other projects, you must do a project report in HTML. In the report you will describe your algorithm and any decisions you made to write your algorithm a particular way. Then you will show and discuss the results of your algorithm. Discuss any extra credit you did, and clearly show what contribution it had on the results (e.g. performance with and without each extra credit component). Feel free to add any other information you feel is relevant.
Rubric
- +10 pts: Create multi-scale filter bank and masks
- +20 pts: Filter, cluster, and compute texton maps
- +20 pts: Compute tg and bg
- +10 pts: Assign pb score to each pixel location
- +10 pts: Evaluate and report F-score (must beat provided baseline method)
- +20 pts: Writeup.
- up to 15 pts of extra credit
- -5*n pts: Lose 5 points for every time (after the first) you do not follow the instructions for the hand in format
Web-Publishing Results
All the results for each project will be put on the course website so that the students can see each other's results. In class we will have presentations of the projects and the students will vote on who got the best results. If you do not want your results published to the web, you can choose to opt out. If you want to opt out, email cs143tas[at]cs.brown.edu saying so.
Handing in
This is very important as you will lose points if you do not follow instructions. Every time after the first that you do not follow instructions, you will lose 5 points. The folder you hand in must contain the following:
- README - text file containing anything about the project that you want to tell the TAs but is not appropriate for the writeup webpage
- code/ - directory containing all your code for this assignment
- html/ - directory containing all your html report for this assignment, including images (any images not under this directory won't be published)
- html/index.html - home page for your results
Then run: cs143_handin proj2
If it is not in your path, you can run it directly: /course/cs143/bin/cs143_handin proj2
Credits
Project and some code adapted from Berkeley Computer Vision Group. Project description and code by Libin "Geoffrey" Sun and James Hays.