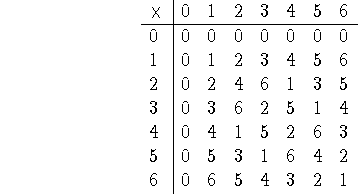
Modular division is trickier. We start with the idea that division is supposed to be the opposite of multiplication. We saw that in mod 7 arithmetic, 5 times 6 yields 2. It follows that 2 divided by 6 should yield 5. This is in fact true.
However, this will not always work. Modulo 15, what is 10 divided by 5? Well, one would think the answer would be 2. On the other hand, since, in an example above, 5 times 5 is 10, perhaps the answer is 5. Then again, in another example above, 8 times 5 is 10, one might say the answer is 8.
Instead of allowing multiple answers, we would say in this case that there is no answer. This is analogous to dividing by zero in regular arithmetic.
The concept of a multiplicative inverse will help us to get an answer when there is one, and will help us to predict when there is no answer. The multiplicative inverse of a number b is the number c such that b times c is 1. In ordinary arithmetic, the multiplicative inverse of b is the reciprocal of b, namely 1/b. For example, let's say we are working with a modulus of 7. The multiplicative inverse of 3 is 5 because 3 times 5 is 1. (For the same reason, the multiplicative inverse of 5 is 3.) We can find multiplicative inverses by building a multiplication table. Here is the table for modulo 7 multiplication.
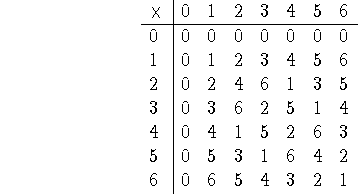
Looking at the table, we see that the multiplicative inverse of 1 is 1, the multiplicative inverse of 2 is 4 (and vice versa), the multiplicative inverse of 3 is 5 (and vice versa), and the multiplicative inverse of 6 is 6. Note that 0 doesn't have a multiplicative inverse. This corresponds to the fact in ordinary arithmetic that 1 divided by 0 does not have an answer.
Now we know how to divide 1 by the different numbers modulo 7: namely, 1 divided by b is the multiplicative inverse of b. How do we divide other numbers? For purposes of this class, the answer is: to divide a by b, just divide 1 by b and then multiply the result by a. For example, let's divide 5 by 4 (modulo 7). Now 1 divided by 4 is 2 because 2 times 4 is 1. We therefore multiply 5 by 2, getting 3. In Mathese,
therefore
therefore
Did this work? Should we accept that 
? Well, multiply
both sides by 4. On the left side, we get 5. On the right side, we
get 
which is indeed congruent to 5.
Below are more mod 7 examples. Check the results by multiplying both sides by the denominator.
For some moduli, some numbers do not have multiplicative inverses. For example, modulo 15, the number 12 does not have a multiplicative inverse. There is no number which when multiplied by 12 gives a result that is congruent mod 15 to 1. If you construct the mod 15 multiplication table, you will find that many other standard names (in particular, 0, 3, 5, 6, 9, and 10) do not have multiplicative inverses. This phenomenon is explored in the next section.
Note, however, that there are still cases where mod 15 division by 12
makes sense. For example, since 
, it
would make sense to define 
to be 9. The number theory
to figure out such fractions is slightly more complicated than the
number theory covered in this class, so we won't ask you to calculate
such divisions.